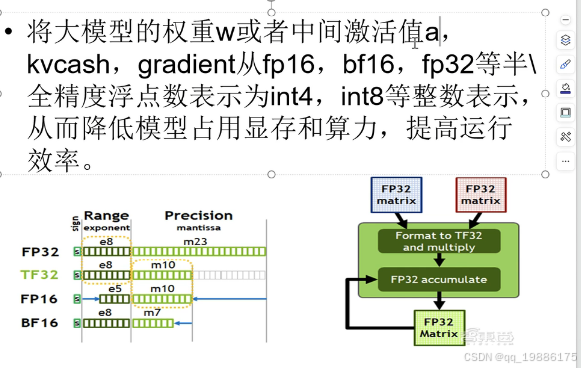
大模型量化常用方法
大模型权重值模型的部署的文件,叫权重。例如LAMMA 70B,权重的参数就有70B个。中间激活值a,就是在推理过程中的中间值。KVcache ,transformer中有K,Q,V三个矩阵。Q是每个token进来,K,V是需要重复计算的,例如我们已经输出了一个token,在输出第二个token的时候还需要计算第一个token的K V计算,说白了就是用内存换取速度的决定。,gradient是梯度,可
什么是量化
大模型权重值模型的部署的文件,叫权重。例如LAMMA 70B,权重的参数就有70B个。
中间激活值a,就是在推理过程中的中间值。
KVcache ,transformer中有K,Q,V三个矩阵。Q是每个token进来,K,V是需要重复计算的,例如我们已经输出了一个token,在输出第二个token的时候还需要计算第一个token的K V计算,说白了就是用内存换取速度的决定。,gradient是梯度,可能也会被量化。但是不一定。
例如这里举个例子:W =W0 + a*g,W0指的是上一步的weight,a是学习率(一般1的-1 -4 -5次方)梯度消失就是g基本为0的,所以W 基本趋于W0,因为计算机内是有精度的,一旦超出了我们的计算机精度,就会造成梯度消失。
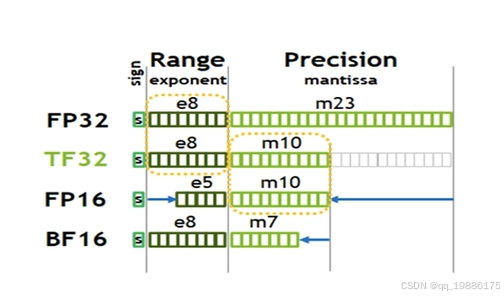
首先来讲一下FP32
FP32(32-bit Single Precision Floating Point)
- 表示方式: 1位符号位 + 8位指数位 + 23位尾数位
- 范围(Range): 大约 10−38次方 到 10的38次方,为什么8位指数位可以表示10的38次方?因为这里是2282^{2^{8}}228,也就是21282^{128}2128次方,换算成10进制就是10的38次方咯
- 精度(Precision): 大约2的-23次方(因为precision部分是23个位置啦~)换算成10进制就是10的-7次方
- 应用: FP32常用于需要高精度的训练和推理任务。
TF32的表示方式啥的都在图中了 。
这里还提到了INT8,int8就是指一个符号位,7个指数位,int4是3个指数位,没有小数位了.
所以如果我们权重从FP32改到int8,int4,那么我们的显存会降低很多。
量化的本质

T指的是未量化之前的占用的宽度,例如说FP32,那么我们这里使用INT 8后尾数位就被量化掉了。如果我们这里用FP16,那么其实我们这里是拓宽了,因为FP16的指数位占5位,而int8占7位。。。
公式化的结果是:
q=clip(round(rs+z),qmin,qmax)q = clip(round(\frac{r}{s}+z),q_{min},q_{max})q=clip(round(sr+z),qmin,qmax)
这里的qmin,qmaxq_{min},q_{max}qmin,qmax指的是要量化的指数位宽度,例如这里我们是要量化为INT 8,那么qmin就是-127,qmax就是127.r是原来的将要被量化的值(例如这里我们要将一个BF16的数把它量化到INT 8,那么r就是BF16类型的),s是量化因子,就是通过缩放多少倍数来把这个数值映射到-127到127这个空间。这里的z是数据偏移的偏执,如果z=0那么叫做对称量化
这里举个例子,从FP16到INT 8的量化:
FP16 值:假设 r=0.75,这是我们的原始 FP16 数值。
缩放因子 s:假设我们选择 s=0.00392(这是一个假定的缩放因子,用于将 FP16 的范围适配到 INT8 的范围)。
零点 z:假设我们使用对称量化(即 z=0)。
计算:
r/s = 0.75/0.00392 = 191.33
取整:对这个值进行四舍五入:
round(191.33)=191
截断:因为 191 在 INT8 的有效范围内(INT8 的范围是 -128 到 127),所以会被截断为 127。
q=clip(191,−128,127)=127
通过这个公式,原本的 FP16 值 0.750.75 被量化为 INT8 的值 127。这个过程主要包括三个步骤:
缩放(通过 scale 使 FP16 的值适配到 INT8 的范围)
平移(通过 zero-point 对非对称量化进行调整)
截断(确保最终的整数值落在 INT8 的范围内)
量化的本质是利用更少的比特数表示更大的浮点数范围,在计算中能够大幅减少存储需求和计算成本。
逐层量化
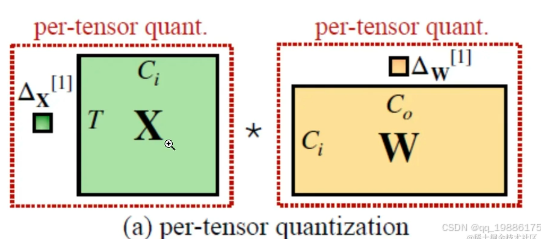
对整个张量使用同一个缩放因子进行量化。每个张量的所有元素在量化时都会被应用相同的缩放因子和零点。这种量化方法简单且高效,因为只需要存储一个缩放因子和零点,但可能在某些情况下牺牲一定的精度。这里举个例子:
假设我们有一个简单的卷积层,输入激活张量 XX 和权重张量 WW 的维度如下:
输入张量 XXX大小为2 x 2,其中的值是浮点数,如:
X=[0.751.2−0.52.0]X = \begin{bmatrix} 0.75 & 1.2 \\ -0.5 & 2.0 \end{bmatrix}X=[0.75−0.51.22.0]
权重张量 W 大小为 2×2,其中的值也是浮点数,如:
W=[0.5−0.751.00.25]W = \begin{bmatrix} 0.5 & -0.75 \\ 1.0 & 0.25 \end{bmatrix}W=[0.51.0−0.750.25]
我们将输入激活 X 和权重 W 量化为 8 位整数(INT8),并选择缩放因子分别为 ΔX=0.01,ΔW=0.02。
1.量化输入张量 X:
Xq=round(XΔX)=round(X0.01)=[75120−50200]X_q = \text{round}\left(\frac{X}{\Delta_X}\right) = \text{round}\left(\frac{X}{0.01}\right) = \begin{bmatrix} 75 & 120 \\ -50 & 200 \end{bmatrix}Xq=round(ΔXX)=round(0.01X)=[75−50120200]
2. 量化权重张量 W:
Wq=round(WΔW)=round(W0.02)=[25−385013]W_q = \text{round}\left(\frac{W}{\Delta_W}\right) = \text{round}\left(\frac{W}{0.02}\right) = \begin{bmatrix} 25 & -38 \\ 50 & 13 \end{bmatrix}Wq=round(ΔWW)=round(0.02W)=[2550−3813]
3进行整数矩阵乘法:
Yq=Xq×Wq=[75120−50200]×[25−385013]Y_q = X_q \times W_q = \begin{bmatrix} 75 & 120 \\ -50 & 200 \end{bmatrix} \times \begin{bmatrix} 25 & -38 \\ 50 & 13 \end{bmatrix}Yq=Xq×Wq=[75−50120200]×[2550−3813]
4 反量化输出结果: 假设乘法的结果是 YqY_qYq=1000,我们将这个整数值反量化回浮点数:
Y=Yq×(ΔX×ΔW)=1000×(0.01×0.02)=0.2Y = Y_q \times \left( \Delta_X \times \Delta_W \right) = 1000 \times (0.01 \times 0.02) = 0.2Y=Yq×(ΔX×ΔW)=1000×(0.01×0.02)=0.2
逐通道和逐标记量化
逐通道量化也叫per-channel quant 。对权重张量的每一个输出通道使用不同的缩放因子。图中的橙色条表示每一个输出通道都对应一个缩放因子 ΔW,这样每个输出通道的量化可以独立处理。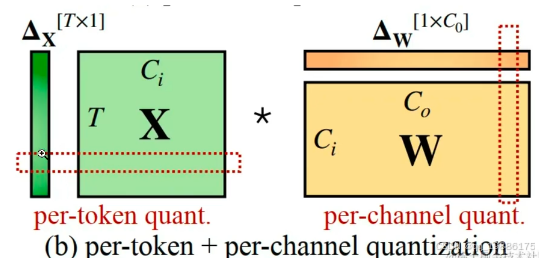 对输入激活张量的每一行(即每个 token)使用不同的缩放因子。图中的绿色竖条表示输入张量 X 每一行都用一个不同的缩放因子 ΔX 进行量化。
对输入激活张量的每一行(即每个 token)使用不同的缩放因子。图中的绿色竖条表示输入张量 X 每一行都用一个不同的缩放因子 ΔX 进行量化。
大模型量化也分为:
- 量化感知训练(Quantization Aware Training, QAT):在模型训练过程中加入伪量化算子,通过训练时统计输入输出的数据范围可以提升量化后模型的精度,适用于对模型精度要求较高的场景;其量化目标无缝地集成到模型的训练过程中。这种方法使LLM在训练过程中适应低精度表示,增强其处理由量化引起的精度损失的能力。这种适应旨在量化过程之后保持更高性能。
- 量化感知微调(Quantization-Aware Fine-tuning,QAF):在微调过程中对LLM进行量化。主要目标是确保经过微调的LLM在量化为较低位宽后仍保持性能。通过将量化感知整合到微调中,以在模型压缩和保持性能之间取得平衡。
- 训练后量化(Post Training Quantization, PTQ):在LLM训练完成后对其参数进行量化,只需要少量校准数据,适用于追求高易用性和缺乏训练资源的场景。主要目标是减少LLM的存储和计算复杂性,而无需对LLM架构进行修改或进行重新训练。PTQ的主要优势在于其简单性和高效性。但PTQ可能会在量化过程中引入一定程度的精度损失。
我们这里主要将训练后量化,训练后量化也分为权重量化和全量化:
权重量化仅量化模型的权重以压缩模型的大小,在推理时将权重反量化为原始的float32数据,后续推理流程与普通的float32模型一致。权重量化的好处是不需要校准数据集,不需要实现量化算子,且模型的精度误差较小,由于实际推理使用的仍然是float32算子,所以推理性能不会提高。
不会提高。
全量化不仅会量化模型的权重,还会量化模型的激活值,在模型推理时执行量化算子来加快模型的推理速度。为了量化激活值,需要用户提供一定数量的校准数据集用于统计每一层激活值的分布,并对量化后的算子做校准。校准数据集可以来自训练数据集或者真实场景的输入数据,需要数量通常非常小。
主流量化方法 LLM.int8
LLM.int8 量化方法是针对大模型进行8-bit 量化的技术,主要用于降低推理过程中内存占用和计算开销,同时尽可能保留模型的精度。在深度学习中,尤其是处理大型语言模型时,模型参数的存储和计算非常耗费资源。通过将模型权重从 32-bit 浮点数(FP32)压缩到 8-bit 整数(INT8),可以大幅度提高推理效率,并减少存储需求。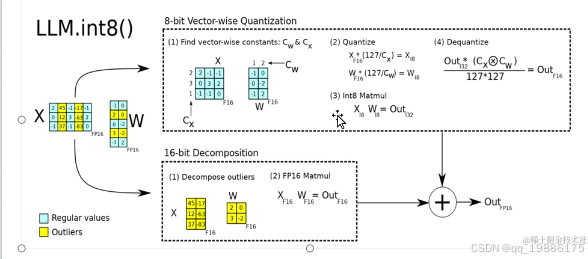
图片的主要部分分为两块:
8-bit 向量量化(8-bit Vector-wise Quantization)
16-bit 异常值分解(16-bit Decomposition)
首先看
8bit向量量化
1、 首先,对于输入矩阵 X 和权重矩阵 W,我们通过一些常量 CX 和 CW 来进行缩放。这些常量用于将浮点数映射到较小的整数范围,即 8-bit 的量化空间。这里的 CX 和 CW 分别用于输入和权重矩阵的缩放。
CX 和 CW 是分别作用在每个矩阵上的缩放常量。
2、量化,通过常量CX CW将矩阵X 和W量化为8bit整数。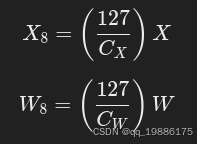 这一步的目的是将浮点数矩阵 X 和 W 转换为整数矩阵 X8 和 W8,以便进行更加高效的矩阵乘法计算。
这一步的目的是将浮点数矩阵 X 和 W 转换为整数矩阵 X8 和 W8,以便进行更加高效的矩阵乘法计算。
3、8bit矩阵乘法
接下来,使用量化后的 8-bit 矩阵 X8 和 W8 进行矩阵乘法。8-bit 的矩阵乘法极大地降低了计算开销,并提高了推理速度:
Out32=X8×W8Out_{32}=X_8×W_8Out32=X8×W8
4、反量化
为了将计算结果恢复到浮点数格式,需要进行反量化。这一步通过乘以缩放因子来恢复浮点结果: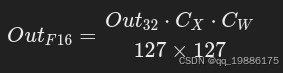
这一操作将 32-bit 的整数结果 Out32 转换回 16-bit 浮点数OutF16,这是为了保证结果可以保持在较高精度的范围内。
16bit异常值分解
在量化过程中,有一些值在范围上超出了 8-bit 整数的表示能力,称为异常值(Outliers)。这些值不能通过简单的 8-bit 量化精确表示,因此需要单独处理。这一步骤通过 16-bit 的方式处理这些异常值,以避免量化误差。
(1) 异常值分解(Decompose outliers)
首先,我们将输入矩阵 XX 和权重矩阵 WW 中的异常值进行分解。这些异常值单独处理,并不会参与 8-bit 的量化计算。
这些被标为黄色的部分即为异常值,它们通过高精度的 FP16 运算处理。
(2) FP16 矩阵乘法(FP16 Matmul)
接下来,对于这些异常值部分,进行 16-bit 精度的矩阵乘法。这一过程保证了计算的精度,即使在量化过程中丢失了一些信息,也可以通过异常值的精确计算来弥补:
最后,将两个结果相加
OutF16=OutF16+OutF16OutliersOut_{F16} = Out_{F16}+Out_{F16}^{Outliers}OutF16=OutF16+OutF16Outliers
GPTQ
GPTQ 尤其适用于推理阶段的优化,因为大语言模型通常有数百亿参数,这使得推理阶段的计算量巨大。GPTQ 技术能够将推理时的计算量减少数倍,使得大模型可以更高效地部署在边缘设备或资源受限的硬件上。
与传统量化方法相比,GPTQ 在以下几个方面进行了创新:
分组量化(Group-wise Quantization)
后量化误差最小化(Post Quantization Error Minimization)
块稀疏性和低比特量化支持
GPTQ需要数据校准,在量化一部分后会有误差,这时候需要数据集来纠正这部分误差。
1、分组量化
在 GPTQ 中,不是对整个矩阵进行统一的量化,而是将模型的权重矩阵切分成多个组,对每个组单独量化。这种分组策略的目的是更好地保持量化后的数值分布和模型精度。
具体地,在每个组内,权重值通常表现出更加相似的数值分布,因此对其进行统一量化可以减少精度损失。而且,组的大小是可调的,组越小,量化误差越容易控制,但计算复杂度也会相应增加。因此,GPTQ 通过分组量化在计算效率和量化精度之间找到了平衡。
分组量化的优点:
减少量化误差:不同的组内数值差异较小,使用统一的量化因子可以更准确地表示数值。
提高推理效率:相比逐层或逐张量化,分组量化的计算复杂度较低,并且能够通过并行处理提高推理速度。
2、 后量化误差最小化(Post Quantization Error Minimization)
GPTQ 的一个核心特性是在量化之后,通过优化算法来最小化量化过程中引入的误差。具体方法包括:
迭代修正误差:在量化之后,GPTQ 会检查每个组中的量化误差,并通过迭代优化调整量化结果,使得最终的误差最小化。这种方法确保即使在低比特宽度的情况下,模型的精度也能够得到保障。
全局误差最小化:在模型的多个层或部分中,GPTQ 不仅仅局限于局部组的误差控制,它还考虑了全局的误差分布。在模型推理中,通过优化整个模型的量化权重,GPTQ 能够进一步减少推理误差。
这一步骤特别重要,因为量化本质上是一个损失精度的过程,而 GPTQ 的优化机制能够显著减少这种损失。
3、 支持低比特量化和块稀疏性(Low-bit Quantization and Block Sparsity)
GPTQ 不仅支持传统的 INT8 量化,还能够支持更低的比特宽度,如 INT4 甚至 INT2。这在一些特定场景中非常有效,因为低比特宽度的表示方法可以显著减少计算量和内存使用。
此外,GPTQ 还能够支持块稀疏性(Block Sparsity),即在权重矩阵中保留一定的稀疏结构。例如,对于某些权重矩阵来说,部分元素对模型输出的贡献较小,GPTQ 可以识别并保留这些稀疏性。在推理过程中,这意味着可以跳过不必要的计算,从而进一步加速模型推理。
块稀疏性和低比特量化的优势:
极大地减少计算量和内存占用:在 INT4 或更低的比特宽度下,计算和存储需求可以显著降低。
推理速度更快:块稀疏性和低比特量化使得推理过程更加高效,尤其适用于大规模模型的部署。

4、GPTQ量化具体过程
-
预处理和分组:首先,GPTQ 对模型中的权重矩阵进行分组。这些组可以根据模型的层结构或者特定的维度进行划分。分组后,GPTQ 对每个组独立地进行量化处理。
-
量化参数计算:对于每个分组,GPTQ 计算该组的量化参数,包括缩放因子(scale)和零点(zero-point)。这些参数用于将浮点数权重映射到整数值。
-
初步量化:使用计算出的量化参数,将组内的浮点数权重量化为低精度的整数表示(如 INT8 或 INT4)。
-
后量化优化:对初步量化后的结果进行误差最小化处理。GPTQ 会使用优化算法来迭代修正量化误差,保证每个组的量化误差尽可能小。
-
稀疏化处理(可选):如果模型允许稀疏性,GPTQ 会在最后一步执行块稀疏处理,进一步减少不必要的计算。
-
推理阶段的量化计算:在推理时,量化后的模型可以直接使用低精度的整数值进行快速矩阵乘法运算。对于稀疏矩阵,推理过程中还可以跳过稀疏部分的计算。
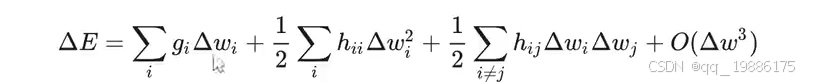
这是GPTQ中用来计算量化误差的公式。在权重 w 发生变化后,模型误差 ΔE 如何变化。该公式主要是通过泰勒展开式来近似计算权重量化后引入的误差。
首先来看第一项:一阶梯度项
∑giΔwi\sum g_i Δw_i∑giΔwi,其中gig_igi是权重 wiw_iwi 对误差函数 E 的一阶导数(梯度),也就是偏导数。它反映了每个权重 wiw_iwi 的变化对总误差的线性影响。ΔwiΔw_iΔwi是权重 wiw_iwi 的量化变化,也就是权重在量化前后的差值。这一项表示的是权重量化引入的线性误差,它描述了权重变化对误差的直接影响。如果 gig_igi 很大,意味着 wiw_iwi 的变化会对总误差 ΔE 产生较大的线性影响。
smoothquant
SmoothQuant 是一种专门针对 Transformer 模型(如 BERT、GPT 等)进行优化,目的是在减少计算资源和加速推理的同时,尽量减少精度损失。与传统量化方法不同,SmoothQuant 引入了一种创新的预处理步骤,称为 平滑缩放(Smooth Scaling),通过平衡权重和激活值的范围,从而使量化更平稳,减少信息丢失。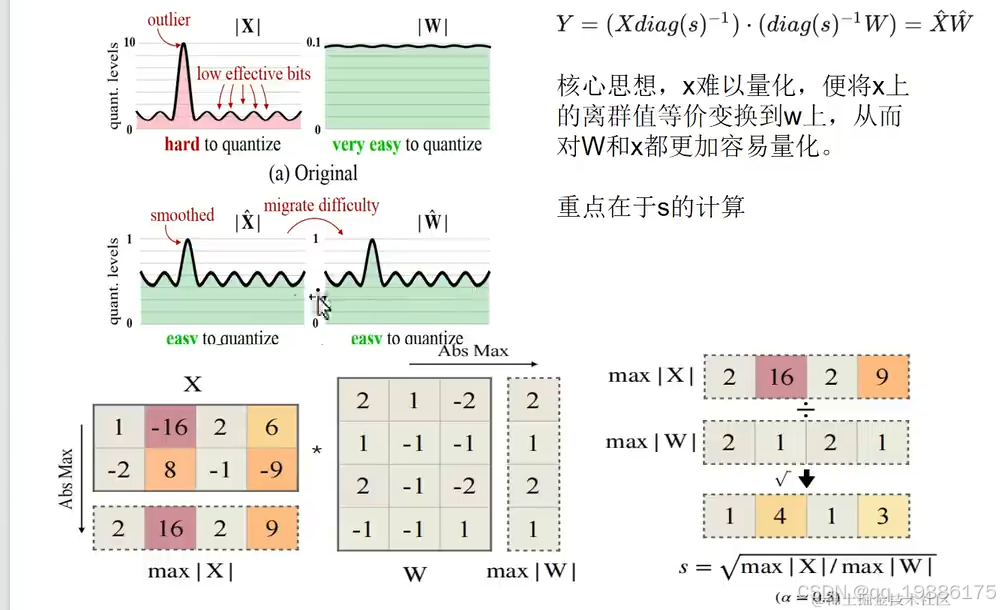
量化流程:
- 提取激活值的尺度因子:计算激活张量中每一层的尺度因子,这个尺度因子反映了激活值的动态范围。激活值的尺度因子可以通过绝对值的统计方法来估计。
- 重新缩放激活值和权重:通过将激活值的尺度因子应用于激活值,并对权重应用反向缩放,使得激活值和权重的动态范围更加一致。
X′=X/ScaleX' = X /ScaleX′=X/Scale
激活值 X 通过尺度因子进行缩放,使其范围缩小。
W′=W∗ScaleW ' = W * ScaleW′=W∗Scale
将相同的尺度因子反向应用于权重 W,使其范围增大。
这样,激活值和权重的乘积保持不变,但它们的动态范围经过了调整,从而减少了量化时的误差。 - 量化激活值和权重:经过缩放之后,激活值和权重的数值范围更加平衡,可以更高效地进行低比特宽度量化(如 INT8)。通常情况下,SmoothQuant 会使用 INT8 进行量化,因为这种格式能够在大幅减少存储和计算开销的同时,保留较高的精度。
- 推理阶段:在推理时,模型会使用量化后的激活值和权重进行计算。这时,激活值和权重已经被平衡化,量化误差也被有效控制。量化后推理的速度大幅提升,尤其是在硬件支持量化加速的场景下(如 TensorRT 或低精度处理器)。
总的来说就是激活值X要除缩放因子s,权重W要乘缩放因子s。那么这个s怎么找呢?
我们这里通过知乎得知: s就是X激活值中最大值/权重W中绝对值的最大值。
s就是X激活值中最大值/权重W中绝对值的最大值。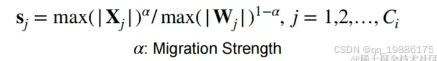
Auto AWQ
Auto AWQ 是一种自动化的权重量化方法,旨在在不显著损失模型推理精度的情况下,通过激活感知来优化权重量化过程。这种方法尤其适用于大规模的预训练模型(如 GPT、BERT 等),以减少其存储和推理的计算开销。
Auto AWQ 自动化了量化过程中最重要的两个部分:
权重选择与分组:权重根据其对模型输出的重要性和激活值分布进行分组,确保关键权重在量化过程中获得更精确的表示。
量化误差补偿:根据激活值的统计分布来调整量化区间和缩放因子,最大限度减少量化误差,从而保证量化模型的推理性能。
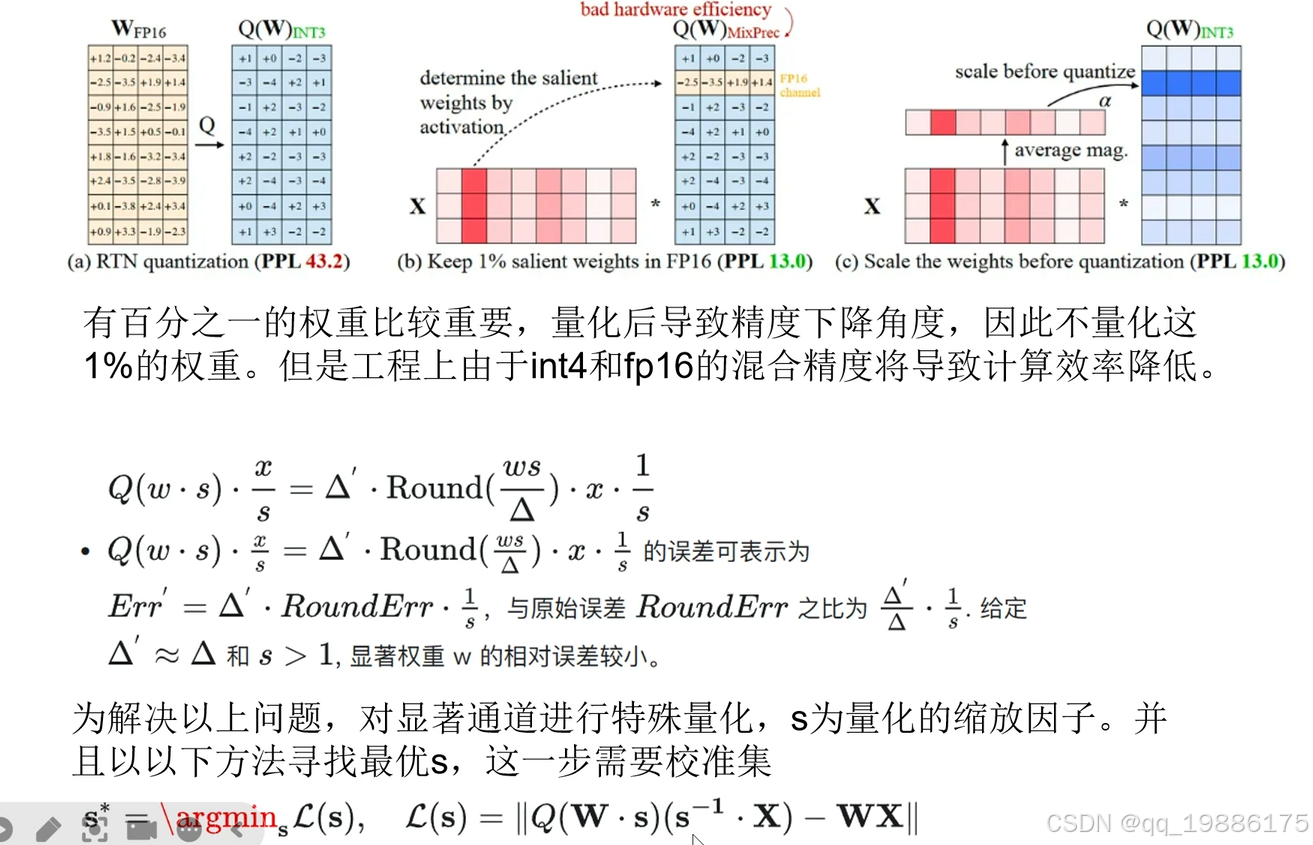 那这1%的重要权重该怎么找呢,基于原论文作者提出三种方式:
那这1%的重要权重该怎么找呢,基于原论文作者提出三种方式:
- 随机挑选
- 基于权重分布挑选
- 基于激活值挑选
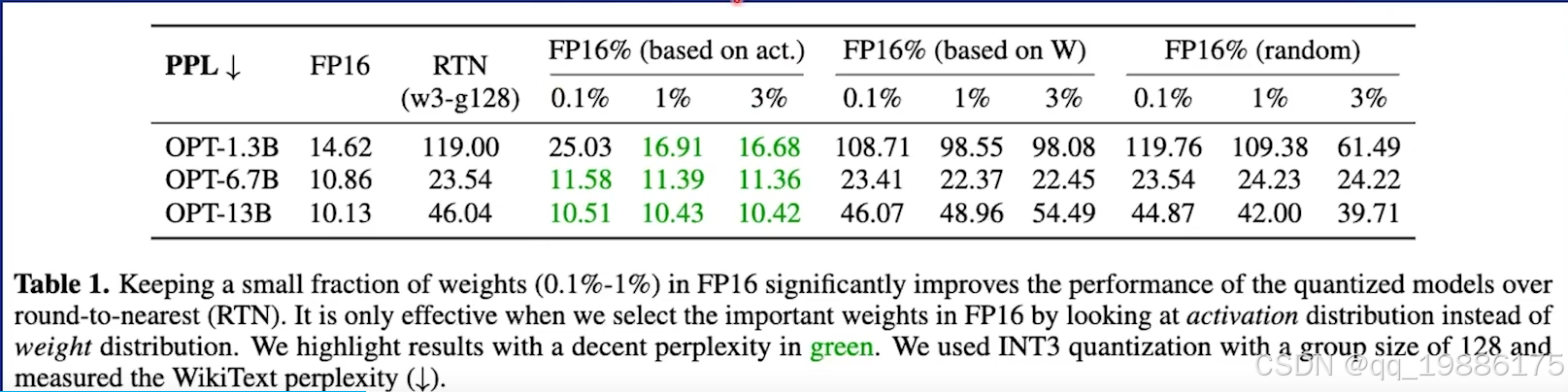 最终结果发现随机挑选困惑度达到100左右,基于权重挑选的话困惑读也在100左右,比随机挑选好一点。基于激活值挑选的话效果一下子好很多,从100+降到20多了。
最终结果发现随机挑选困惑度达到100左右,基于权重挑选的话困惑读也在100左右,比随机挑选好一点。基于激活值挑选的话效果一下子好很多,从100+降到20多了。
所以基于激活值,按通道“组团”挑选显著权重 ,那怎么挑选呢?将激活值对每一列(channel)求绝对值的平均值,把平均值较大的一列对应的权重的通道视作显著权重
这里就对应了上面AWQ开头的c图,放大部分如下: 可以看到左边的激活值第二列就是平均值较大的一列。那什么是平均值较大的一列对应的权重的通道?再看右边这幅图,我们激活值的第二列是比较重要的,在y=wx+by=wx+by=wx+b的时候权重的第二行的元素才跟激活值第二列的权重有关系,其他都没关系的,所以后续我们只需要把这一行进行保持,其他都进行int3量化就可以了。
可以看到左边的激活值第二列就是平均值较大的一列。那什么是平均值较大的一列对应的权重的通道?再看右边这幅图,我们激活值的第二列是比较重要的,在y=wx+by=wx+by=wx+b的时候权重的第二行的元素才跟激活值第二列的权重有关系,其他都没关系的,所以后续我们只需要把这一行进行保持,其他都进行int3量化就可以了。
但是实现的过程中还是有点问题的,我们显著的阈值是什么?这个评判标准如何设置?还有如何实现在后续计算过程中有的是FP16,有的是int ,这个对硬件和其他开发者非常不友好。基于此问题,作者又提出了一种方法。
量化时对显著权重进行放大可以降低量化误差
我们先看下原始权重量化公式:
考虑权重矩阵www,线性运算写作y=wxy=wxy=wx,对权重矩阵进行量化后可以写作y=Q(w)xy=Q(w)xy=Q(w)x.Q(`)的定义如下:
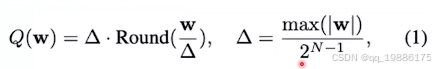
这个delta 表示权重绝对值的最大值除2N−12^{N-1}2N−1,这个N就由量化精度决定,如果int4量化那N就等于3.delta就是量化单位
那么经过优化的公式(引入缩放因子)如下: 这里的 s>1是一个缩放因子,用来对权重进行缩放。缩放的目的是让权重的分布更加适合量化,以减少量化带来的误差。
这里的 s>1是一个缩放因子,用来对权重进行缩放。缩放的目的是让权重的分布更加适合量化,以减少量化带来的误差。
公式表示通过缩放 w 之后,再通过类似的量化公式对缩放后的 w 进行量化。最后,乘以输入 x 并除以缩放因子 s,以保持正确的运算结果。
可以看到从效果上跟第一个传统公式是一样的,但是作者表示引入缩放因子是可以减少误差的,为什么? 左侧部分的量化误差公式
左侧部分的量化误差公式 RoundErr(w/Δ)RoundErr(w/ Δ)RoundErr(w/Δ) 表示在四舍五入过程中产生的误差。因为量化后的结果是对权重进行了离散化,所以一定会存在四舍五入带来的误差。这个总的量化误差是 Δ乘RoundErr四舍五入后的误差在乘输入x。
RoundErr(w/Δ)RoundErr(w/ Δ)RoundErr(w/Δ) 表示在四舍五入过程中产生的误差。因为量化后的结果是对权重进行了离散化,所以一定会存在四舍五入带来的误差。这个总的量化误差是 Δ乘RoundErr四舍五入后的误差在乘输入x。
当权重值较小时,量化步长 Δ 越大,四舍五入带来的误差也会越大。因此,在标准量化的情况下,较大的权重变化范围可能导致较大的误差。
右侧部分是引入缩放因子的量化误差: 这里的量化误差公式为:
这里的量化误差公式为:
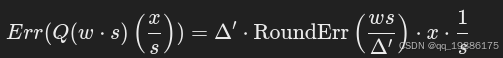 我们这里是对那1%重要的权重进行量化,即使他们乘s,在众多权重元素中可能 Δ依旧不变, Δ只跟max(|w|)和量化精度有关。
我们这里是对那1%重要的权重进行量化,即使他们乘s,在众多权重元素中可能 Δ依旧不变, Δ只跟max(|w|)和量化精度有关。
所以 Δ‘跟 Δ很大概率都一样的。所以跟入s后,RoundErr的分子变大,分母基本不变。相当于分母变大,分子不变。进而导致误差减小咯。缩放后的值最终再通过 1\s 调整回原来的范围。因此,整体量化误差会小于不使用缩放因子的情况。
所以最终的量化方式是:所有权重均低比特量化,显著权重*较大s,等效于降低量化误差。非显著权重乘较小s,等效于基于更少关注。
(a) RTN quantization:
1. 这表示传统的 RTN(Round-to-Nearest)量化方法,其将权重矩阵 WFP16WFP16 中的权重直接舍入为整数形式(如 INT3)。
2. RTN 的问题在于无法很好地处理高维稀疏矩阵,尤其是图中所示的红色代表“关键”权重,它们对推理精度影响较大,简单地舍入这些权重会导致较大的精度下降,表现为右侧图中的 PPL(perplexity)上升到 43.2。
(b) Keep 1% salient weights in FP16:
- 该部分描述了一种混合精度量化策略,将最重要的 1% 权重保留为原精度(FP16),而量化剩余权重为 INT3。红色区域表示未量化的关键权重,通过这种方法可以避免精度大幅下降。
- 虽然这种方法提升了模型的精度(PPL 从 43.2 降到了 13.0),但由于存在不同的精度表示,计算效率相对较低(称为“bad hardware efficiency”),因为硬件难以高效处理混合精度的计算。
(c ) Scale the weights before quantization:
- 在量化前对权重进行缩放(通过系数 α),可以使得权重的分布更适合低精度量化,最终量化为 INT3。这种方法保持了高计算效率,同时进一步降低了 PPL(perplexity)到 13.0。
- 这个策略结合了缩放因子和整体的量化过程,确保了在同一精度下的硬件计算效率最大化。
 这个公式展示了权重w在缩放因子下的量化,其中s是缩放因子。在量化过程中也会引起误差,例如GPTQ引入校准数据集,那么AWQ这里为了降低误差引入量化误差公式:
这个公式展示了权重w在缩放因子下的量化,其中s是缩放因子。在量化过程中也会引起误差,例如GPTQ引入校准数据集,那么AWQ这里为了降低误差引入量化误差公式: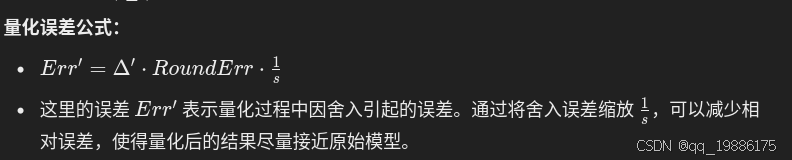
都说缩放因子非常重要,那么怎么找缩放因子?下面是缩放因子的优化公式:

更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)