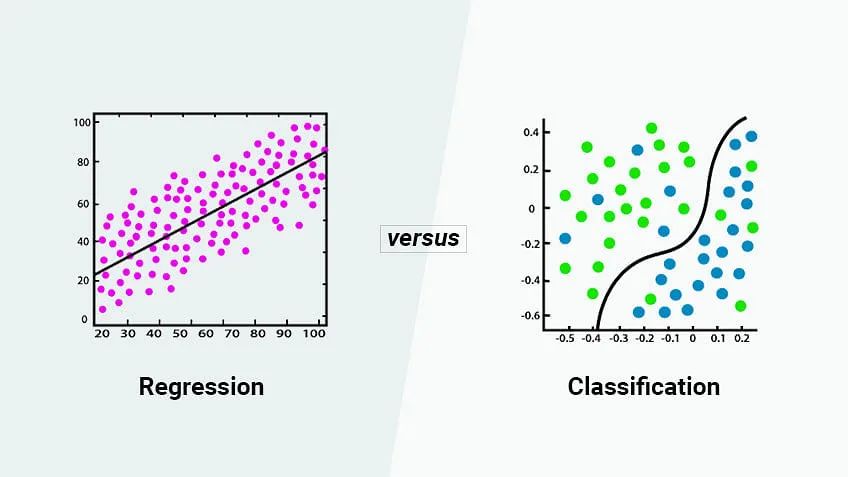
回归（Regression）是机器学习中的一种基本方法，其目标是通过分析自变量与因变量之间的关系，建立一个数学模型来预测因变量的值。

线性回归、多项式回归、正则化线性回归是机器学习中常用的回归分析方法。其中线性回归用直线拟合数据关系，多项式回归用曲线拟合复杂关系，正则化线性回归通过加约束来防止模型过于复杂。

前排提示，文末有大模型AGI-CSDN独家资料包哦！

Regression

一、线性回归

线性回归（Linear Regression）是什么？线性回归是一种统计方法，用于建模两个或多个变量之间的关系。它假设因变量和自变量之间的关系是线性的，并试图找到最小化误差平方和的最佳拟合直线。

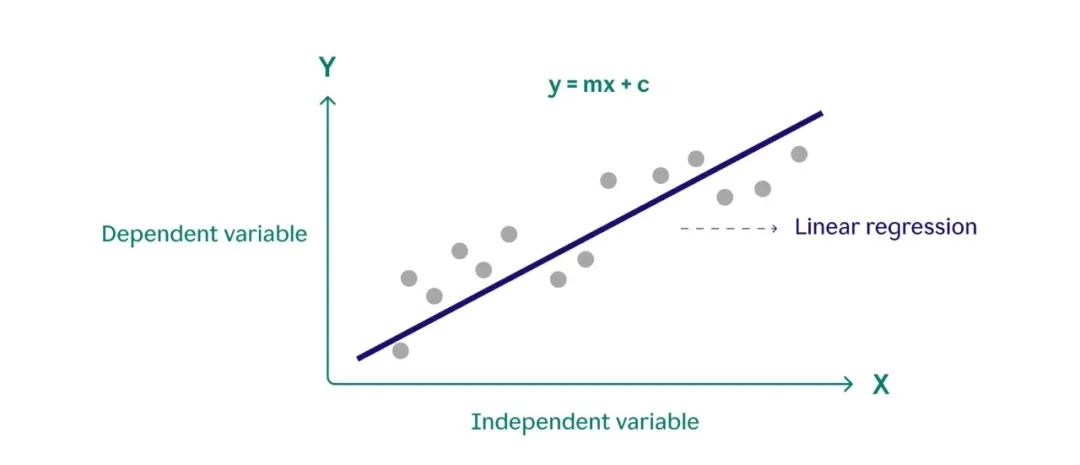
如何实现线性回归模型并进行可视化？在Python中实现一个线性回归模型并进行可视化，可以使用scikit-learn库来拟合模型，并使用matplotlib库来进行可视化。

import numpy as np``import matplotlib.pyplot as plt``from sklearn.linear_model import LinearRegression``from sklearn.model_selection import train_test_split``   ``# 生成一些示例数据``np.random.seed(0)  # 设置随机种子以获得可重复的结果``X = 2 * np.random.rand(100, 1)  # 生成100个0到2之间的随机数作为自变量``y = 4 + 3 * X + np.random.randn(100, 1)  # 生成因变量，其中加入了随机噪声``   ``# 将数据集拆分为训练集和测试集``X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)``   ``# 创建线性回归模型并拟合训练数据``model = LinearRegression()``model.fit(X_train, y_train)``   ``# 使用模型进行预测``y_pred = model.predict(X_test)``   ``# 可视化结果``plt.scatter(X, y, color='blue', label='Data Points')  # 绘制数据点``plt.plot(X_test, y_pred, color='red', linewidth=2, label='Regression Line')  # 绘制回归线``plt.xlabel('X')``plt.ylabel('y')``plt.legend()``plt.title('Linear Regression')``plt.show()``   ``# 打印模型参数``print(f'Intercept: {model.intercept_[0]}')``print(f'Coefficient: {model.coef_[0][0]}')

二、多项式回归

多项式回归（Polynomial Regression）是什么？多项式回归是线性回归的一种推广，它允许因变量和自变量之间存在非线性关系。通过在传统的线性回归模型中增加变量的高次项（如平方项、立方项等），来捕捉数据中的非线性关系。

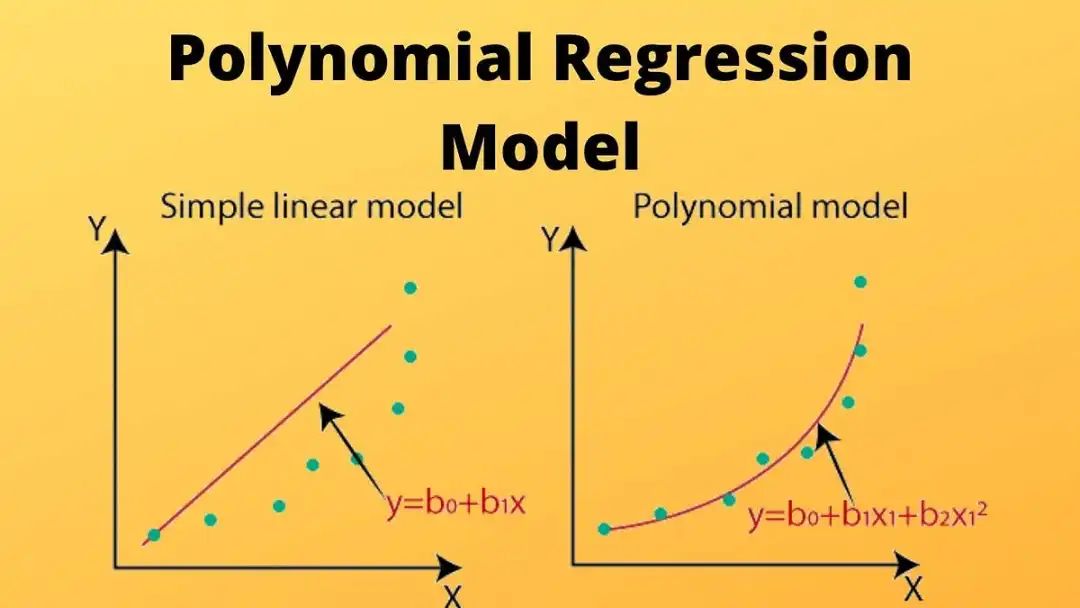
如何实现多项式回归模型并进行可视化？在Python中实现多项式回归模型并进行可视化，可以使用numpy来生成数据和计算多项式特征，scikit-learn的LinearRegression来拟合模型，以及matplotlib来进行可视化。

import numpy as np``import matplotlib.pyplot as plt``from sklearn.linear_model import LinearRegression``from sklearn.preprocessing import PolynomialFeatures``   ``# 生成一些示例数据``np.random.seed(0)``X = np.sort(5 * np.random.rand(40, 1), axis=0)  # 生成40个0到5之间的随机数并排序作为自变量``y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])  # 生成因变量，其中加入了随机噪声``   ``# 定义多项式的次数``degree = 3``   ``# 创建多项式特征``poly = PolynomialFeatures(degree)``X_poly = poly.fit_transform(X)``   ``# 创建线性回归模型并拟合多项式特征数据``model = LinearRegression()``model.fit(X_poly, y)``   ``# 使用模型进行预测``X_test = np.linspace(0, 5, 100).reshape(-1, 1)  # 生成测试数据``X_test_poly = poly.transform(X_test)``y_pred = model.predict(X_test_poly)``   ``# 可视化结果``plt.scatter(X, y, color='blue', label='Data Points')  # 绘制数据点``plt.plot(X_test, y_pred, color='red', linewidth=2, label='Polynomial Regression')  # 绘制多项式回归曲线``plt.xlabel('X')``plt.ylabel('y')``plt.legend()``plt.title(f'Polynomial Regression (degree={degree})')``plt.show()``   ``# 打印模型参数（可选）``# 由于多项式回归的系数较多，这里只打印出来供参考，通常不会直接解释这些系数``print("Model coefficients:", model.coef_)``print("Model intercept:", model.intercept_)

三、正则化线性回归

正则化线性回归（Regularized Linear Regression）是什么？正则化线性回归是一种用于处理线性回归模型过拟合问题的技术。通过在模型的损失函数中引入额外的惩罚项，限制模型参数的大小，从而减少过拟合的风险。

正则化线性回归类型有哪些？岭回归侧重于通过最小化参数平方和来防止模型过拟合，尤其适用于处理共线性问题；Lasso回归则强调稀疏性，通过推动参数变为零来实现特征选择；弹性网络回归结合了岭回归和Lasso回归的特点，平衡了正则化项，既处理过拟合又进行特征选择。

如何实现正则化线性回归模型并进行可视化？在Python中实现正则化线性回归模型并进行可视化，可以使用scikit-learn库来实现岭回归（Ridge Regression）、Lasso回归以及弹性网络回归（Elastic Net Regression），并使用matplotlib库来可视化结果。

import numpy as np``import matplotlib.pyplot as plt``from sklearn.linear_model import Ridge, Lasso, ElasticNet``from sklearn.preprocessing import StandardScaler``from sklearn.pipeline import make_pipeline``from sklearn.model_selection import train_test_split``   ``# 生成示例数据``np.random.seed(0)``X = 2 * np.random.rand(100, 1) - 1  # 生成-1到1之间的随机数作为自变量``y = 4 + 3 * X + np.random.randn(100, 1) * 0.5  # 生成因变量，加入随机噪声``   ``# 标准化数据（对于Lasso和ElasticNet很重要）``scaler = StandardScaler()``X_scaled = scaler.fit_transform(X)``   ``# 拆分数据集为训练集和测试集``X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)``   ``# 定义正则化参数``alpha = 1.0``   ``# 创建岭回归模型并拟合数据``ridge = Ridge(alpha=alpha)``ridge.fit(X_train, y_train)``   ``# 创建Lasso回归模型并拟合数据``lasso = Lasso(alpha=alpha)``lasso.fit(X_train, y_train)``   ``# 创建弹性网络回归模型并拟合数据（这里使用l1_ratio=0.5表示L1和L2正则化的混合）``elastic_net = ElasticNet(alpha=alpha, l1_ratio=0.5)``elastic_net.fit(X_train, y_train)``   ``# 使用模型进行预测``X_test_scaled = scaler.transform(X_test)  # 注意：测试数据也需要经过相同的标准化处理``y_pred_ridge = ridge.predict(X_test_scaled)``y_pred_lasso = lasso.predict(X_test_scaled)``y_pred_elastic_net = elastic_net.predict(X_test_scaled)``   ``# 可视化结果``plt.scatter(X_test, y_test, color='blue', label='Data Points')  # 绘制数据点``plt.plot(X_test, y_pred_ridge, color='red', linewidth=2, label='Ridge Regression')  # 绘制岭回归线``plt.plot(X_test, y_pred_lasso, color='green', linewidth=2, label='Lasso Regression')  # 绘制Lasso回归线``plt.plot(X_test, y_pred_elastic_net, color='purple', linewidth=2, label='Elastic Net Regression')  # 绘制弹性网络回归线``plt.xlabel('X')``plt.ylabel('y')``plt.legend()``plt.title('Regularized Linear Regression')``plt.show()

读者福利：如果大家对大模型感兴趣，这套大模型学习资料一定对你有用

对于0基础小白入门：

如果你是零基础小白，想快速入门大模型是可以考虑的。

一方面是学习时间相对较短，学习内容更全面更集中。
二方面是可以根据这些资料规划好学习计划和方向。

包括：大模型学习线路汇总、学习阶段，大模型实战案例，大模型学习视频，人工智能、机器学习、大模型书籍PDF。带你从零基础系统性的学好大模型！

😝有需要的小伙伴，可以保存图片到wx扫描二v码免费领取【保证100%免费】🆓

👉AI大模型学习路线汇总👈

大模型学习路线图，整体分为7个大的阶段：（全套教程文末领取哈）

第一阶段： 从大模型系统设计入手，讲解大模型的主要方法；

第二阶段： 在通过大模型提示词工程从Prompts角度入手更好发挥模型的作用；

第三阶段： 大模型平台应用开发借助阿里云PAI平台构建电商领域虚拟试衣系统；

第四阶段： 大模型知识库应用开发以LangChain框架为例，构建物流行业咨询智能问答系统；

第五阶段： 大模型微调开发借助以大健康、新零售、新媒体领域构建适合当前领域大模型；

第六阶段： 以SD多模态大模型为主，搭建了文生图小程序案例；

第七阶段： 以大模型平台应用与开发为主，通过星火大模型，文心大模型等成熟大模型构建大模型行业应用。

👉大模型实战案例👈

光学理论是没用的，要学会跟着一起做，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

👉大模型视频和PDF合集👈

观看零基础学习书籍和视频，看书籍和视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

👉学会后的收获：👈

• 基于大模型全栈工程实现（前端、后端、产品经理、设计、数据分析等），通过这门课可获得不同能力；

• 能够利用大模型解决相关实际项目需求： 大数据时代，越来越多的企业和机构需要处理海量数据，利用大模型技术可以更好地处理这些数据，提高数据分析和决策的准确性。因此，掌握大模型应用开发技能，可以让程序员更好地应对实际项目需求；

• 基于大模型和企业数据AI应用开发，实现大模型理论、掌握GPU算力、硬件、LangChain开发框架和项目实战技能， 学会Fine-tuning垂直训练大模型（数据准备、数据蒸馏、大模型部署）一站式掌握；

• 能够完成时下热门大模型垂直领域模型训练能力，提高程序员的编码能力： 大模型应用开发需要掌握机器学习算法、深度学习框架等技术，这些技术的掌握可以提高程序员的编码能力和分析能力，让程序员更加熟练地编写高质量的代码。

👉获取方式：

😝有需要的小伙伴，可以保存图片到wx扫描二v码免费领取【保证100%免费】🆓