1.含理想运放电路的分析方法

通常都会用到“虚断”和“虚短”的性质（规则），并将其灵活运用到结点电压法或回路电流法等一般分析方法中去。正如此前提出的，因运放输出端的电流不确定，所以一般不列输出端结点的KCL方程。

对包含理想运放基础应用电路（如反相比例放大器、加法器、跟随器等）的较复杂电路，可视给定条件合理使用这些应用电路的已知结论（主要是输入输出电压关系）。

2.含非理想运放电路分析注意事项

⑴在一定条件下可使用“虚短”和“虚断”规则

①若非理想运放的关键参数可认为趋于“理想”，该运放的作用近似为理想运放时，则可以按照理想运放电路进行分析。

②只使用“虚短”规则：运放的输入电阻$R_i$有限，但放大倍数$A\to \infty$，“虚短”仍然成立。

③只使用“虚断”规则：运放的放大倍数$A$有限，但输入电阻$R_i\to \infty$，“虚断”仍然成立。

⑵采用运放的线性模型进行电路分析

若不能近似为理想运放，也不具备部分使用“虚短”和“虚断”的条件，则可通过运放的线性模型进行分析和求解，具体方法参考上一篇对非理想运放构成的反相放大器的分析例。

综合题★★★

题1 图1所示电路当$R_L$为何值时获得最大功率？求此最大功率。

图1

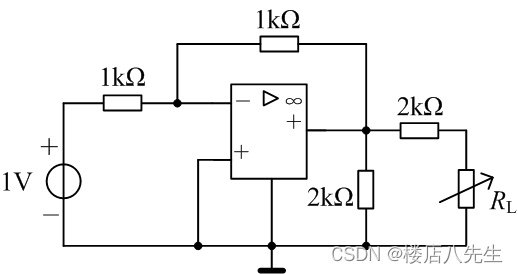
解析：求$R_L$以外电路的戴维宁等效电路，由理想运放的“虚短”、“虚断”可得
$$U_{oc}=-1\text{V，}{I}_{sc}=\frac{-1\mathrm{V}}{2000\mathrm{k}\Omega }=0.5\mathrm{mA}$$
$$\therefore R_{eq}=\frac{U_{oc}}{I_{sc}}=2\mathrm{k}\Omega$$
故，当$R_L=R_{eq}=2\mathrm{k}\Omega$时，该电路获得最大功率
$$P_{max}=\frac{U_{oc}^2}{4R_{eq}}=1.25\times 10^{-4}\mathrm{W}$$

题2 电路如图2所示，求当负载$R_L=10\mathrm{k}\Omega$时负载电流$I_L$的值。

图2

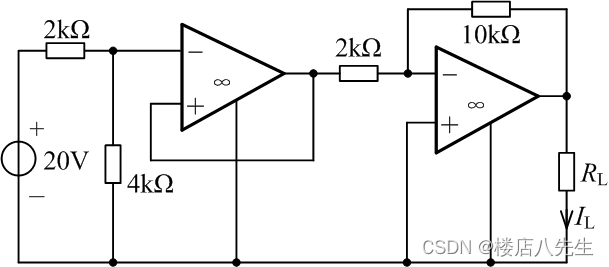
解析：标注电路如图3所示，由“虚短”、“虚断”可知

图3

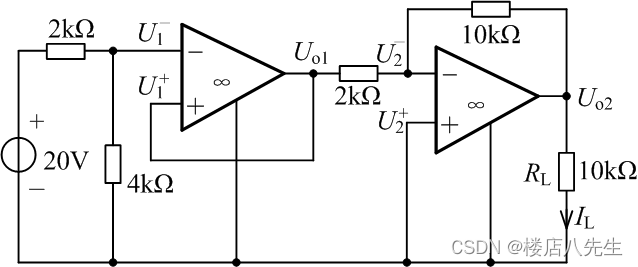
$$U_{o1}=U_1^{-}=\frac{4}{2+4}\times 20\mathrm{V}=\frac{40}{3}\mathrm{V}$$

$$U_{o2}=U_2^{-}-10\times 10^3\times \frac{U_{o1}-U_2^{-}}{2000}=0-5\times \frac{40}{3}\mathrm{V}=-\frac{200}{3}\mathrm{V}$$

$$\therefore I_L=\frac{U_{o2}}{R_L}=\frac{-\frac{200}{3}\mathrm{V}}{10\mathrm{k}\Omega }=-\frac{200}{3}\times 10^{-4}\mathrm{A}=-\frac{20}{3}\mathrm{mA}$$

题3 求图4所示电路的$u_o$。

图4

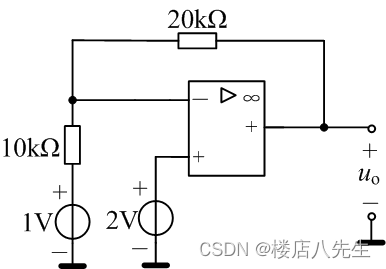
解析：由叠加定理，1V电压源单独作用时电路为反相放大器
$$u_o^{(1)}=-\frac{20}{10}\times 1\mathrm{V}=-2\mathrm{V}$$
2V电压源单独作用时电路为同相放大器
$$u_o^{(2)}=\left(1+\frac{20}{10}\right)\times 2\mathrm{V}=6\mathrm{V}$$
因此
$$u_o=u_o^{\left(1\right)}+u_o^{\left(2\right)}=4\mathrm{V}$$

挑战★★★★★

题4 含运放的电阻电路如图5所示，分别在⑴ $R_{in}=\infty$ ，$A\ne \infty$；⑵$R_{in}=\infty$，$A=\infty$两种情况下，计算开路电压$u_o$、从电压源$u_s$两端看进去的输入电阻$R_i$以及输出电阻$R_{out}$。

图5

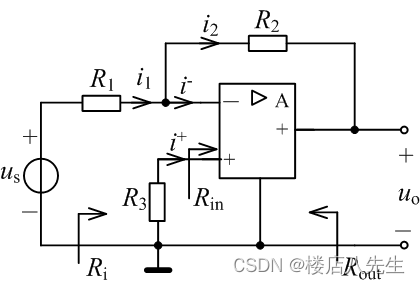
解析：

⑴$R_{in}=\infty$，$A\ne \infty$，为非理想运放应用电路

①求开路电压$u_o$。

图6

因$R_{in}=\infty$，故“虚断”成立，$i^{-}=i^{+}=0$，$i_1=i_2$，参考图6，列回路II和回路I的KVL方程
$$u_s=R_1{i}_1-u_d-R_3{i}^{+}=R_1{i}_1-\frac{u_o}{A}$$
$$u_o=-R_2{i}_2-u_d-R_3{i}^{+}=-R_2{i}_2-\frac{u_o}{A}$$

由以上两式，可得
$$i_1=i_2=\frac{u_s+\frac{u_o}{A}}{R_1}$$
$$u_o=\frac{-R_2/R_1}{1+\frac{R_1+R_2}{A{R}_1}}\cdot u_s=\frac{-A{R}_2}{(1+A)R_1+R_2}\cdot u_s$$

②求输入电阻$R_i$。由①的结果
$$i_1=\frac{u_s+\frac{u_o}{A}}{R_1}=\frac{u_s}{R_1}+\frac{1}{A{R}_1}\cdot \frac{-A{R}_2}{\left(1+A\right)R_1+R_2}\cdot u_s=\frac{1+A}{\left(1+A\right)R_1+R_2}\cdot u_s$$
故，输入电阻
$$R_i=\frac{u_s}{i_1}=R_1+\frac{R_2}{1+A}$$

③求输出电阻$R_{out}$。

把独立源置零，在输出端加电流源$i_s$，如图7所示。

图7

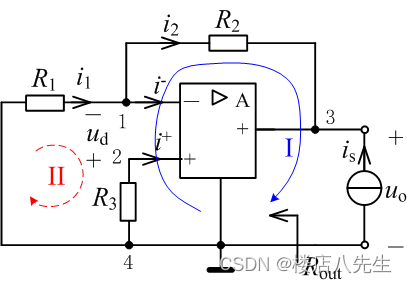
对回路I和回路II列KVL
$$u_o=-R_2{i}_2-u_d-R_3{i}^{+}=-R_2{i}_2-\frac{u_o}{A}$$
$$R_1{i}_1-u_d=R_1{i}_1-\frac{u_o}{A}=0$$
又因为$i_1=i_2$，由以上两式可得
$$\left(1+\frac{R_1+R_2}{A{R}_1}\right)u_o=0$$
在$1+\frac{R_1+R_2}{A{R}_1}\ne 0$的情况下，有$u_o=0$，故输出电阻为
$$R_{out}=\frac{u_o}{i_s}=0$$
⑵$R_{in}=\infty$，$A=\infty$，为理想运放应用电路

①求开路电压$u_o$。

方法一：可将第⑴问中所得$u_o$求$A\to \infty$时的极限值，即
$$u_o=\underset{A\to \infty }{\lim }\frac{-A{R}_2}{\left(1+A\right)R_1+R_2}\cdot u_s=-\frac{R_2}{R_1}{u}_s$$
方法二：可由理想运放的“虚短”、“虚断”直接推导
$$\frac{u_s}{R_1}=-\frac{u_o}{R_2}\Rightarrow u_o=-\frac{R_2}{R_1}{u}_s$$
方法三：电路为理想运放构成的反相放大器，可根据输入输出电压关系直接写出结果。

②求输入电阻$R_i$，由“虚短”、“虚断”，有$u^{-}=u^{+}=0$，故$u_s=R_1{i}_1$，得
$$R_i=\frac{u_s}{i_1}=R_1$$
③求输出电阻$R_{out}$，方法同第⑴问，参考图7，$u_o=-R_2{i}_2=-R_2{i}_1$，而此时$i_1=0$，所以$u_o=0$。故输出电阻$R_{out}$。

更多文集，欢迎关注下方公众号！