论文原文
利用自编码器做协同过滤，协同过滤主要有如下两种情景

• user-based：userA和userB臭味相投，那么A喜欢看的电影可以推荐给B
• item-based: movieX和movieY比较相似，那么用喜欢看movieX，那么可以将movieY也推荐给他

Rating matrix

比如在电影推荐场景中，用户对电影（item）的打分可以构成一个$R\in {\mathbb{R}}^{m\times n}$矩阵：

• 行向量：m个user， u ∈ U = { 1 … m } u \in U=\{1 \ldots m\} u∈U={1…m}，其中每个user可以表示为${\mathbf{r}}^{(u)}=\left(R_{u1},\dots R_{un}\right)\in {\mathbb{R}}^n$，表示该用户对各个item的打分
• 列向量：n个item， i ∈ I = { 1 … n } i \in I=\{1 \ldots n\} i∈I={1…n}，其中每个item可以表示为${\mathbf{r}}^{(i)}=\left(R_{1i},\dots R_{mi}\right)\in {\mathbb{R}}^m$，表示该item在各个用户下被打的分

模型训练

AutoEncoder的思想就是用输出当做label,如下图所示，这是一个item-based场景下的AutoRec模型，输入$r^{(i)}$为$ite{m}^i$对应的$m$维向量，分别作为输出和输出，输入层通过权重$V$得到隐藏层，再通过权重$W$到输出层，通过训练更新参数矩阵$W$和$V$使得输入输出尽可能的相同。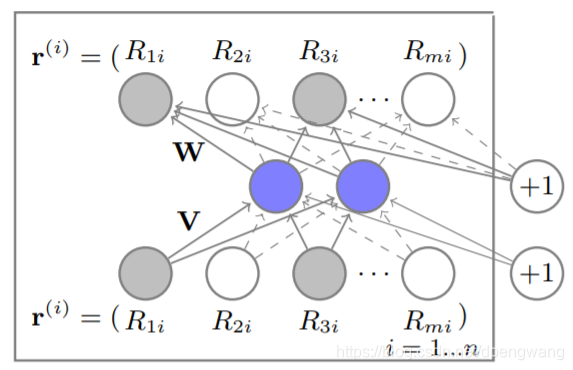

损失函数

AutoRec模型的损失函数如下所示
$$\underset{\theta }{\min }\sum _{i=1}^n{\Vert {\mathbf{r}}^{(i)}-h\left({\mathbf{r}}^{(i)};\theta \right)\Vert }_{\mathcal{O}}^2+\frac{\lambda }{2}\cdot \left(\Vert \mathbf{W}{\Vert }_F^2+\Vert \mathbf{V}{\Vert }_F^2\right)$$其中$\Vert \cdot {\Vert }_{\mathcal{O}}^2$表示只对观测到的数据去损失函数，即在Rating Matrix中，没有打分的部分不管他，encode decode的过程中只让模型去拟合已有的打分部分，让这一部分充分拟合好，然后对于没有数据的部分，训练好的权重会给出一个非零值，这就是模型预测的结果。

最终，原来Rating Matrix中为零的部分在模型训练完后也变也有了数值，可以根据此来做推荐。