简单的神经元模型

线性神经元

其函数表达如下所示：

<script type="math/tex; mode=display" id="MathJax-Element-79">y=b+\sum_ix_iw_i</script>
其中，ww<script type="math/tex" id="MathJax-Element-80">w</script>表示权值，x $x$<script type="math/tex" id="MathJax-Element-81">x</script>表示输入。yy<script type="math/tex" id="MathJax-Element-82">y</script>表示输出。
线性神经元模型中，输入xi可以被看作是 来自其他神经元的动作电位，该动作电位引起突触的兴奋。权重 wi 可以认为是对突触的影响系数。wi 的值越大，输入xi对神经元输出的影响程度就越大。在一个真正的神经元中，某些因素能够决定 wi可以是突触vescicles中的突触前末梢的数量，或配体门控通道在突触后膜的数量。

二进制阈值神经元

二进制阈值神经元可以表示为：

<script type="math/tex; mode=display" id="MathJax-Element-320">y= \begin{cases} 输入值>阈值& \text{= 1}\\ 输入值<阈值& \text{= 0} \end{cases}</script>
简单的如果输入值小于阈值，则输出结果为0，如果输入值大于阈值，则输出结果为1.

Rectified Linear Neurons(ReLu)

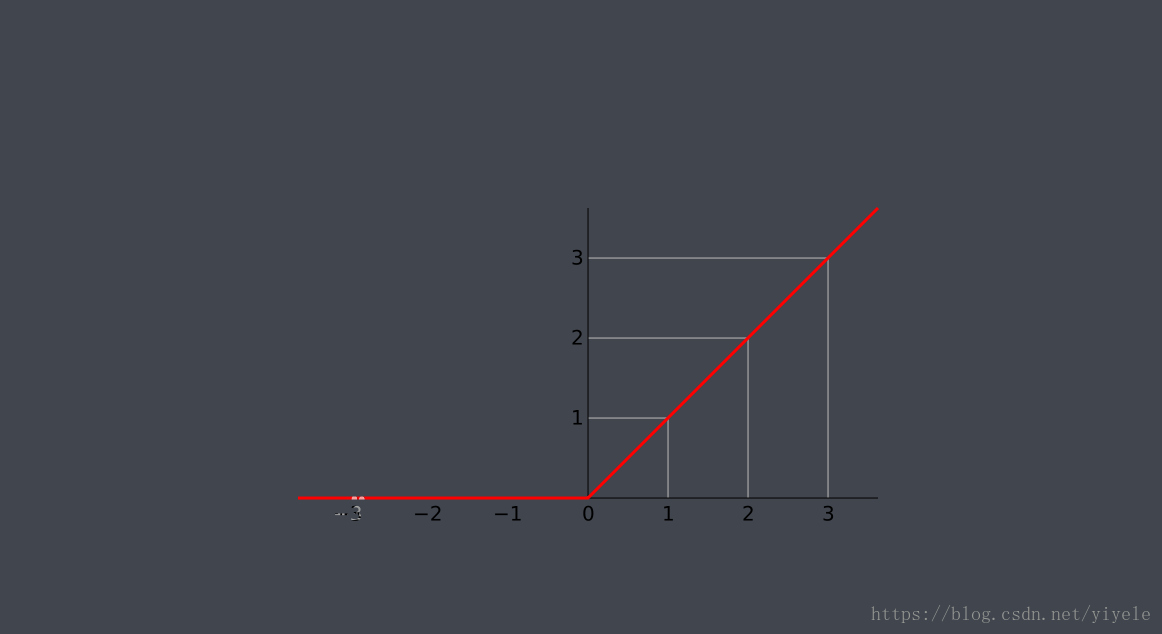
综合第一种神经元和第二种神经元可以得到ReLu。具体函数表达式如下所示：

<script type="math/tex; mode=display" id="MathJax-Element-325">z=b+\sum_ix_iw_i</script>
<script type="math/tex; mode=display" id="MathJax-Element-326">y= \begin{cases} z& \text{if z > 0}\\ 0& \text{otherwise} \end{cases}</script>
具体如下图所示：

sigmoid neurons

具体函数表达如下所示：

<script type="math/tex; mode=display" id="MathJax-Element-229">z=b+\sum_ix_iw_i</script>
<script type="math/tex; mode=display" id="MathJax-Element-230">y=\frac{1}{1+exp(-z)}</script>
具体如下图所示：

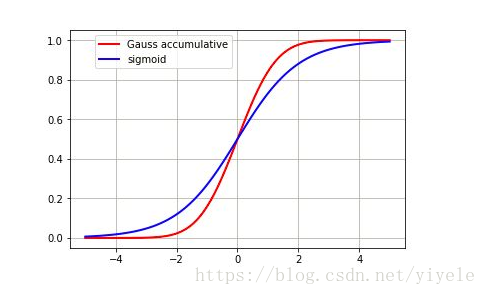
优点：使用逻辑回归函数，并且导数光滑。
缺点：计算量大。

随机二进制神经元

具体函数表达如下所示：

<script type="math/tex; mode=display" id="MathJax-Element-295">z=b+\sum_ix_iw_i</script>
<script type="math/tex; mode=display" id="MathJax-Element-296">p(s=1)=\frac{1}{1+exp(-z)}</script>
输出值是1或0，如果值很大，则可能输出1（有很大概率），如果值很小，则输出值可能是0（有很大概率）。