---

前言

本篇文章主要记录自动驾驶控制算法学习中的一些基础的非模型优化的算法，包括纯跟踪算法（PurePursuit）、Stanley算法、后轮反馈控制算法。

---

一、纯跟踪算法

1. 车辆运动学模型

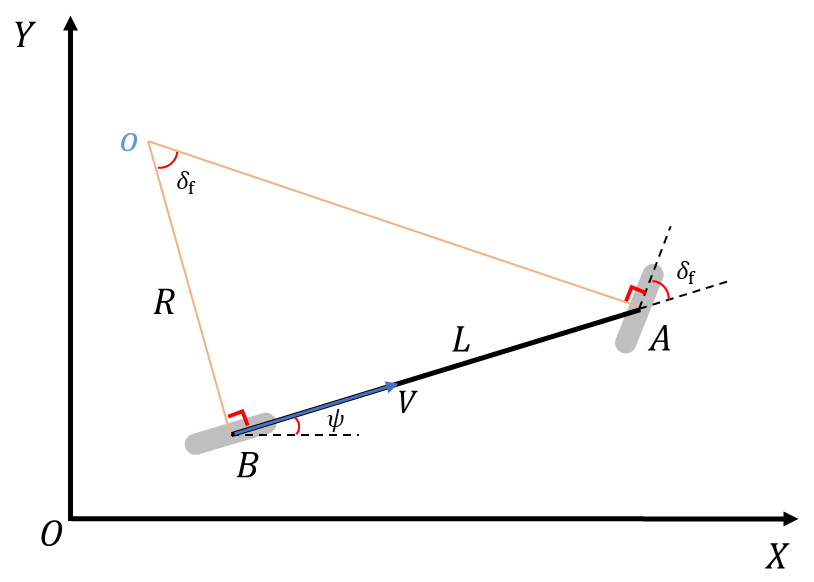
纯跟踪算法采用基于车辆后轴中心的运动学模型，此处假定后轮不转向。

模型中的符号和定义如下：

$A$：前轮中心点；$B$：后轮中心点；（左右轮都合并为单个轮子）
${\delta }_f$：前轮转向角；
$L$：车辆轴距；
$V$：车辆的速度；
$O$：车辆的瞬时旋转中心；
$R$：车辆的轨迹半径；
$\Psi$：车辆的航向角；

基于车辆后轴中心的运动学模型为：
$$\begin{array}{r}\dot{X}=V\cos \Psi \\ \dot{Y}=V\sin \Psi \\ \dot{\Psi }=\frac{V\tan {\delta }_f}{L}\end{array}$$
前轮转向角和后轴跟随曲线之间的几何关系可表示为：
$$\begin{array}{r}\tan {\delta }_f=\frac{L}{R}\end{array}$$

2. 纯跟踪算法推导

纯追踪算法的原理为通过调整前轮转向角${\delta }_f$，使得车辆后轴中心刚好可以经过规划路径中给定的路径点。可以理解为，以车辆后轮沿当前点与给定路径点构成的圆弧行驶。

图中的部分符号和定义如下：
$P$：车辆追踪的规划路径中的目标点；
$r$：车辆后轴中心与目标点组成的圆弧的半径；
$\alpha$：后轴中心到目标点的向量与车身坐标系的夹角；
$e_y$：目标点在车身坐标系下的横向偏差；

前轮转向角和后轴跟随曲线之间的几何关系可知，计算前轮转角需计算出车辆后轴中心点的路径半径$R$，当$R=r$时，车辆的后轴中心经过目标点。
在三角形$△oPB$中，由正弦定理可得：
$$\begin{array}{r}\frac{\sin 2\alpha }{l_d}=\frac{\sin (\frac{\pi }{2}-\alpha )}{r}\end{array}$$
由$\sin (\frac{\pi }{2}-\alpha )=\cos \alpha$，$\sin 2\alpha =2\sin \alpha \cos \alpha$，将上式整理可得：
$$\begin{array}{r}r=\frac{l_d}{2\sin \alpha }\end{array}$$

由$\tan {\delta }_f=\frac{L}{R}$，令$R=r$，可得前轮转角的表达式为：
$$\begin{array}{r}{\delta }_f=\arctan \frac{2\sin (\alpha )L}{l_d}\end{array}$$
其中，$\alpha$为后轴中心到目标点的向量与车身坐标系的夹角，方向根据车身参考系的设定进行判断，本文章设定为左正右负。

拓展：
由上图可知$\sin \alpha =\frac{e_y}{l_d}$，带入上式可得：

$$\begin{array}{r}r=\frac{l_d^2}{2e_y}\end{array}$$

由$\tan {\delta }_f=\frac{L}{R}$，令$R=r$，可得：
$$\begin{array}{r}{\delta }_f=\arctan \frac{2e_{y}L}{l_d^2}\end{array}$$
其中目标点在车身坐标系下的横向偏差$e_y$可通过向量运算求得，已知目标点$P(x_p,y_p)$到车辆后中心点$B(x_b,y_b)$的向量为$\overrightarrow{PB}=(x_p-x_b,y_p-y_b)$，沿车辆速度方向的单位向量$\vec{k}=(\cos \Psi ,\sin \Psi )$：
$$\begin{array}{r}{e}_y=\left|\overrightarrow{PB}\times \vec{k}\right|\end{array}$$

二、Stanley算法

1.车辆运动学模型

Stanley同样采用与纯跟踪算法相同的运动学模型-基于车辆后轴中心的运动学模型，Stanley算法中使用前轴中心的信息可通过几何转换获得。

2.Stanley算法推导

图中的部分符号和定义如下：
$A、B$：车辆前轴、后轴中心点；
$P$：规划路径中距前轴中心最近的点；
$L$：车辆轴距；
$v$：车辆前轮速度；
$\Psi$：车辆航向角；
${\Psi }_t$：$P$点处的航向角；
${\delta }_f$：车辆的前轮转角；
${\delta }_e$：车辆前轮转角与$P$点处航向角之间的偏差；
${\Psi }_e$：$P$点处航向角与车辆航向角之间的偏差；
$e_y$：前轴中线点到$P$点切线方向的偏差；
$d$：车辆速度方向与$P$点切线方向的交点与前轴中心点沿$P$点切线方向的纵向偏差；

Stanley算法是一种基于前轮航迹误差($e_y$)的非线性反馈控制算法，由上图中的几何关系可得：
$$\begin{array}{r}{\Psi }_e={\Psi }_t-\Psi \end{array}$$
前轮速度方向与目标点航向偏差的表达式为：
$$\begin{array}{r}{\delta }_e=\arcsin \frac{k\cdot e_y}{v}=\arctan \frac{e_y}{d}\end{array}$$
其中$k$为算法中设定的系数。
上式表明，当车辆沿速度方向行驶至与目标点$P$切线方向相交位置时，车辆前轮航迹偏差为0。对上述三角形来说，速度值不变的情况下，系数k越大，车辆前轮航迹偏差减少的速度越快。
此外可得$d$与系数$k$反相关，与速度$v$的大小正相关。在小角度的情况下，可近似得：$d\approx \frac{v}{k}$

综上可得，车辆前轮转角控制量${\delta }_f$计算公式为：
$$\begin{array}{r}{\delta }_f={\Psi }_t-\Psi +\arcsin \frac{k\cdot e_y}{v}\end{array}$$

拓展:横向误差变化率分析
车辆横向误差变化率为：
$$\begin{array}{r}{\dot{e}}_y=-v\sin {\delta }_e\end{array}$$
此处假设$e_y$，${\delta }_e$为标量，在正确的控制下，横向误差会越来越小，因此横向偏差变化率为负。
根据几何关系可得：
$$\begin{array}{r}\sin {\delta }_e=\frac{e_y}{\sqrt{d(t{)}^2+e_y^2}}\end{array}$$
根据$d\approx \frac{v}{k}$，上式可写为：
$$\begin{array}{r}\sin {\delta }_e=\frac{k\cdot e_y}{\sqrt{v^2+(k{e}_y{)}^2}}\end{array}$$
进而可得：
$$\begin{array}{r}{\dot{e}}_y=-\frac{k\cdot e_y}{\sqrt{1+(\frac{k{e}_y}{v}{)}^2}}\end{array}$$
当横向误差很小时，上式可改写为：
$$\begin{array}{r}{\dot{e}}_y=-k\cdot e_y\end{array}$$
对上式进行积分可得：
$$\begin{array}{r}{e}_y(t)=e_y(0)\cdot e^{-kt}\end{array}$$
当$t⟶\infty$时，横向误差以指数形式收敛于0，参数$k$决定了收敛速度。

三、后轮位置反馈控制算法

1.车辆运动学模型

后轮位置反馈控制同样采用与纯跟踪算法相同的运动学模型-基于车辆后轴中心的运动学模型。

2.后轮位置反馈控制算法推导

图中的部分符号和定义如下：
$A、B$：车辆前轴、后轴中心点；
$P$：规划路径中距后轴中心最近的点；
$L$：车辆轴距；
$v$：车辆后轴中心处的速度；
$\dot{s}$：目标点处的速度；
$\Psi$：车辆航向角；
${\Psi }_t$：$P$点处的航向角；
${\delta }_f$：车辆的前轮转角；
${\psi }_e$：$P$点处航向角与车辆航向角之间的偏差；
$e_y$：前轴中线点到$P$点切线方向的偏差；
$d$：后轴中心点到目标点的距离；

车辆的横向位置误差$e_y$可通过向量法计算，已知目标点$P(x_p,y_p)$到车辆后中心点$B(x_b,y_b)$的向量为$\overrightarrow{PB}=(x_p-x_b,y_p-y_b)$，沿路径点切线方向的单位向量$\vec{k}=(\cos {\psi }_t,\sin {\psi }_t)$：
$$\begin{array}{r}{e}_y=\left|\overrightarrow{PB}\times \vec{k}\right|\end{array}$$
当车辆后轴中心点位于路径对应车辆前进方向左侧时，$e_y$为正，反之为负。在上图所示情况下，$e_y$为负。

航向角误差${\psi }_e$为车辆航向角$\psi$与目标点处航向角${\psi }_t$的差值：
$$\begin{array}{r}{\psi }_e={\psi }_t-\psi \end{array}$$
假设以路径曲线在目标点处的旋转中心为$o$，车辆后轴中心角速度${\omega }_r$和目标点处的角速度${\omega }_s$近似相等，根据车辆旋转角速度计算公式$\frac{V}{R}$可得：
$$\begin{array}{r}\frac{\dot{s}}{R}=\frac{v\cdot \cos {\psi }_e}{R-e_y}\end{array}$$
在上图所示情况下，目标点处的曲率$k(s)$为正，旋转半径$R=\frac{1}{k(s)}$为正，$e_y$为负。
则$\dot{s}$的表达式可写为：
$$\begin{array}{r}\dot{s}=\frac{v\cdot \cos {\psi }_e}{1-k(s)\cdot e_y}\end{array}$$
车辆横向移动的速度$\dot{e}$可写为：
$$\begin{array}{r}{\dot{e}}_y=v\cdot \sin {\psi }_e\end{array}$$

车辆航向角误差的变化率${\dot{\psi }}_e$可写为：
$$\begin{array}{r}{\dot{\psi }}_e=\dot{\psi }-{\dot{\psi }}_t\end{array}$$
由${\dot{\psi }}_t=\frac{\dot{s}}{R}=\dot{s}\cdot k(s)$，带入上式可得：
$$\begin{array}{r}{\dot{\psi }}_e=\dot{\psi }-\frac{v\cdot k(s)\cdot \cos {\psi }_e}{1-k(s)\cdot e_y}\end{array}$$
综上，目标点处的速度、横向误差变化率、航向误差变化率的微分方程形式整理如下：
$$\begin{array}{r}\dot{s}=\frac{v\cdot \cos {\psi }_e}{1-k(s)\cdot e_y}\\ {\dot{e}}_y=v\cdot \sin {\psi }_e\\ {\dot{\psi }}_e=\dot{\psi }-\frac{v\cdot k(s)\cdot \cos {\psi }_e}{1-k(s)\cdot e_y}\end{array}$$

李亚普洛夫稳定判据

基于上述微分方程，定义李亚普洛夫函数形式如下：
$$\begin{array}{r}V(e_y,{\psi }_e)=\frac{1}{2}{e}_y^2+\frac{1}{2\cdot k_2}{\psi }_e^2\end{array}$$
其中$k_2>0$，为了使$(e_y,{\psi }_e)$在平衡点$(0,0)$处稳定，根据李亚普洛夫稳定判据，必须满足以下两个条件：

1. ${\lim }_{|e_y,{\psi }_e|\to \infty }V=\infty$
2. $\dot{V}<0(e_y\ne 0,{\psi }_e\ne 0)$
   对于条件1，定义的李亚普洛夫函数显式成立，所以李亚普洛夫稳定判据第一条满足。
   对于$\dot{V}<0$，结合上述推导的微分方程，推导形式如下：

$$\begin{array}{r}\dot{V}=e_y\cdot {\dot{e}}_y+\frac{1}{k_2}\cdot {\psi }_e\cdot {\dot{\psi }}_e\\ =e_y\cdot v\cdot \sin ({\psi }_e)+\frac{1}{k_2}\cdot {\psi }_e\cdot (\dot{\psi }-\frac{v\cdot k(s)\cdot \cos {\psi }_e}{1-k(s)\cdot e_y})\end{array}$$
令$\dot{V}=0$，得临界控制率${\dot{\psi }}^{\ast }$表达式如下：
$$\begin{array}{r}{\dot{\psi }}^{\ast }=\frac{v\cdot k(s)\cdot \cos ({\psi }_e)}{1-k(s)\cdot e_y}-\frac{k_2\cdot v\cdot e_y\sin ({\psi }_e)}{{\psi }_e}\end{array}$$

为满足李亚普洛夫稳定判据第2条，设置一个调节函数$g(e_y,{\psi }_e,t)=k_{\psi }|v|>0$，可以得出基于航向角变化率的控制命令：
$$\begin{array}{r}\dot{\psi }={\dot{\psi }}^{\ast }-k_{\psi }\cdot |v|\cdot {\psi }_e\end{array}$$
将上式带入$\dot{V}$的表达式可得：
$$\begin{array}{r}\dot{V}=\frac{k_{\psi }}{k_2}\cdot |v|\cdot {\psi }_e^2\le 0\end{array}$$
所以设计的控制率满足稳定性条件。

根据车辆几何关系：
$$\begin{array}{r}\tan {\delta }_f=\frac{L}{R}\end{array}$$
车辆航向变化率、车速、转弯半径的关系为$\dot{\psi }=\frac{V}{R}$，结合上式可得车辆前轮转角为：
$$\begin{array}{r}{\delta }_f=\arctan \frac{\dot{\psi }\cdot L}{v}\end{array}$$
其中：
$$\begin{array}{r}\dot{\psi }=\frac{v\cdot k(s)\cdot \cos ({\psi }_e)}{1-k(s)\cdot e_y}-\frac{k_2\cdot v\cdot e_y\sin ({\psi }_e)}{{\psi }_e}-k_{\psi }\cdot |v|\cdot {\psi }_e\end{array}$$

---

参考文献

1、自动驾驶决策规划控制
2、控制算法