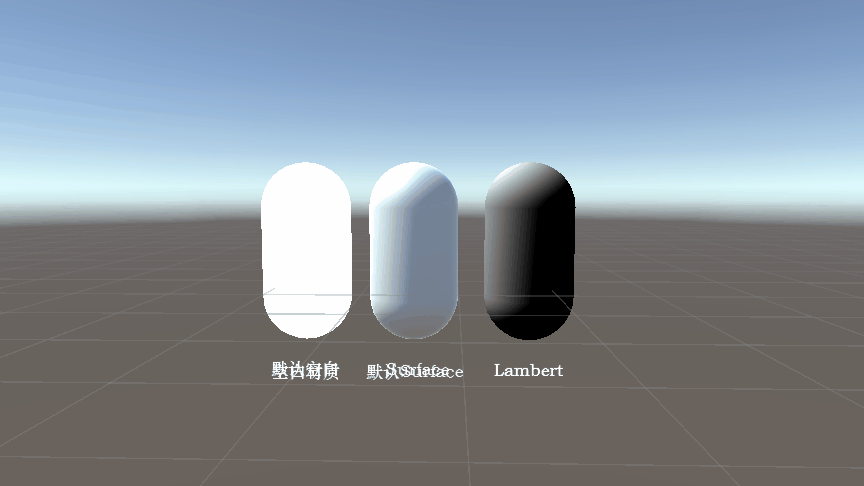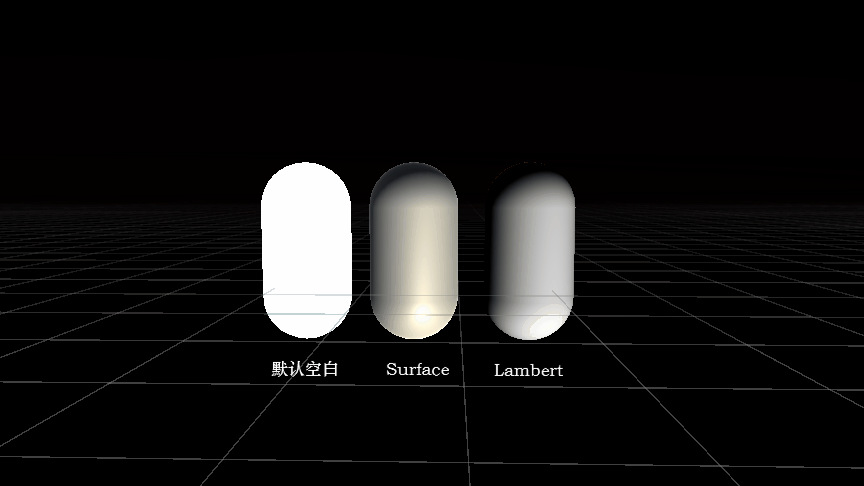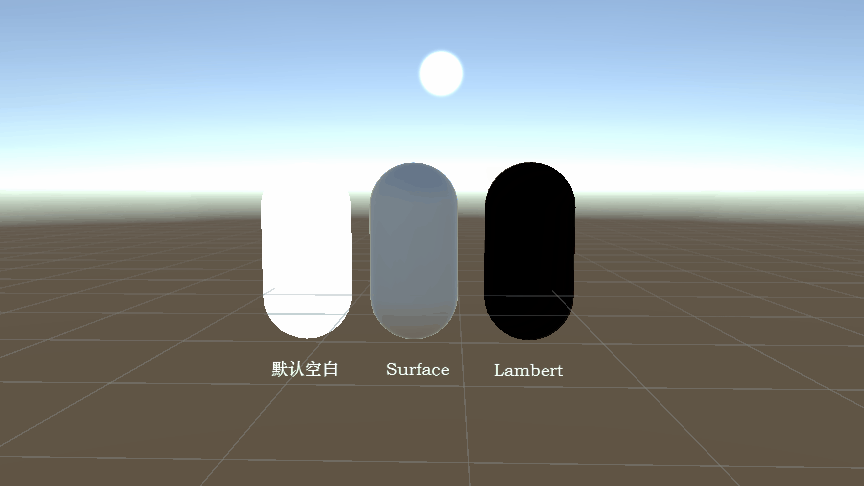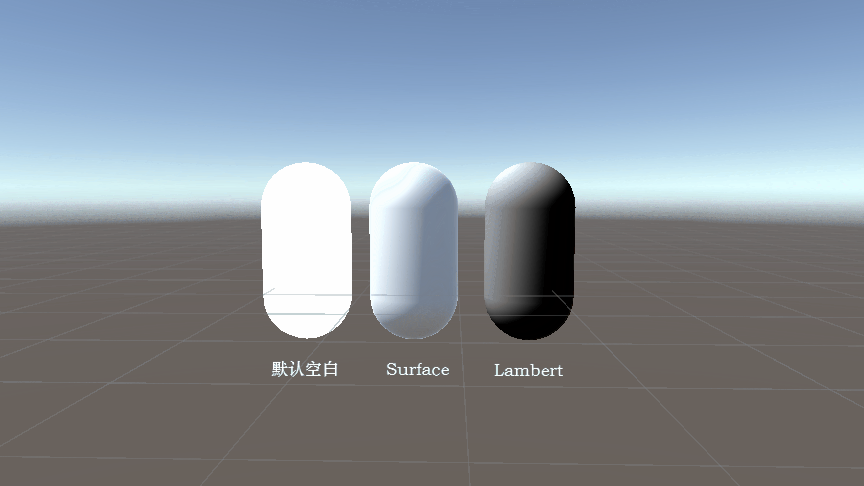
Unity Shader 代码结构解析：以 Lambert 光照模型为例

引言

Shader 是 Unity 中实现图形渲染的核心工具，而理解 Shader 的代码结构是掌握 Shader 编程的第一步。本文将以 Lambert 光照模型为例，详细解析 Unity Shader 的代码结构，帮助你从零开始理解 Shader 的编写逻辑。

---

1. Unity Shader 的基本结构

Unity Shader 的代码通常分为以下几个部分：

1. Shader 声明：定义 Shader 的名称和路径。
2. Properties 块：定义 Shader 的属性，这些属性可以在 Unity Inspector 面板中调整。
3. SubShader 块：包含一个或多个 Pass，每个 Pass 代表一次渲染过程。
4. Pass 块：包含顶点 Shader 和片段 Shader 的代码。
5. CGPROGRAM 块：编写 HLSL 代码的地方。

以下是一个简单的 Unity Shader 框架：

Shader "Custom/MyShader"
{
    Properties
    {
        // 属性定义
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 200

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            // HLSL 代码
            ENDCG
        }
    }
    FallBack "Diffuse"
}

接下来，我们将逐步解析这个结构，并以 Lambert 光照模型为例，填充具体的代码。

---

2. Shader 声明

Shader 声明定义了 Shader 的名称和路径。例如：

Shader "Custom/MyShader"

这行代码表示 Shader 的名称为 MyShader，路径为 Custom/MyShader。你可以在 Unity 的材质面板中选择这个 Shader。

---

3. Properties 块

Properties 块定义了 Shader 的属性，这些属性可以在 Unity Inspector 面板中调整。例如：

Properties
{
    _MainTex ("Texture", 2D) = "white" {}
    _Color ("Color", Color) = (1,1,1,1)
}

• _MainTex 是一个 2D 纹理属性，默认值为白色。
• _Color 是一个颜色属性，默认值为白色。

---

4. SubShader 块

SubShader 块包含一个或多个 Pass，每个 Pass 代表一次渲染过程。例如：

SubShader
{
    Tags { "RenderType"="Opaque" }
    LOD 200

    Pass
    {
        CGPROGRAM
        #pragma vertex vert
        #pragma fragment frag

        // HLSL 代码
        ENDCG
    }
}

• Tags 定义了 Shader 的渲染类型和层级。
• LOD 表示 Shader 的细节级别（Level of Detail），用于性能优化。

---

5. Pass 块

Pass 块是 Shader 的核心部分，包含顶点 Shader 和片段 Shader 的代码。例如：

Pass
{
    CGPROGRAM
    #pragma vertex vert
    #pragma fragment frag

    // HLSL 代码
    ENDCG
}

• #pragma vertex vert 指定顶点 Shader 函数为 vert。
• #pragma fragment frag 指定片段 Shader 函数为 frag。

---

6. CGPROGRAM 块

CGPROGRAM 块是编写 HLSL 代码的地方。以下是实现 Lambert 光照模型的完整代码：

Shader "Custom/LambertShader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _Color ("Color", Color) = (1,1,1,1)
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 200

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float3 worldNormal : TEXCOORD1;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;
            float4 _Color;

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);  // 顶点变换
                o.worldNormal = UnityObjectToWorldNormal(v.normal);  // 法线变换
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);  // 纹理坐标变换
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);  // 光源方向
                float3 normal = normalize(i.worldNormal);  // 法线方向
                float diff = max(dot(normal, lightDir), 0);  // 漫反射强度
                fixed4 col = tex2D(_MainTex, i.uv) * _Color * diff;  // 最终颜色
                return col;
            }
            ENDCG
        }
    }
    FallBack "Diffuse"
}

6.1 顶点 Shader

顶点 Shader 的主要任务是将顶点从模型空间转换到裁剪空间，并计算法线方向：

v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);  // 顶点变换
    o.worldNormal = UnityObjectToWorldNormal(v.normal);  // 法线变换
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);  // 纹理坐标变换
    return o;
}

• UnityObjectToClipPos 将顶点从模型空间转换到裁剪空间。
• UnityObjectToWorldNormal 将法线从模型空间转换到世界空间。
• TRANSFORM_TEX 处理纹理坐标的缩放和偏移。

6.2 片段 Shader

片段 Shader 的主要任务是计算每个像素的颜色。在 Lambert 光照模型中，我们通过点积计算漫反射强度：

fixed4 frag (v2f i) : SV_Target
{
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);  // 光源方向
    float3 normal = normalize(i.worldNormal);  // 法线方向
    float diff = max(dot(normal, lightDir), 0);  // 漫反射强度
    fixed4 col = tex2D(_MainTex, i.uv) * _Color * diff;  // 最终颜色
    return col;
}

• dot(normal, lightDir) 计算法线与光源方向的夹角。
• max(..., 0) 确保漫反射强度非负。
• tex2D 对纹理进行采样。

---

7. 附录：Lambert光照模型原理详解

在 Unity Shader 编程中，光照模型是决定物体表面如何与光线交互的核心部分。Lambert 光照模型是最基础且常用的光照模型之一，它模拟了光线在物体表面均匀散射的效果。

7.1 光照模型简介

光照模型用于描述光线与物体表面交互的方式。常见的光照模型包括：

• Lambert 漫反射模型：模拟光线均匀散射的效果。
• Phong 高光反射模型：模拟镜面反射的高光效果。
• Blinn-Phong 模型：Phong 模型的改进版，计算效率更高。

Lambert 光照模型是最简单的漫反射模型，适用于模拟粗糙表面的光照效果。

---

7.2 Lambert 光照模型的物理基础

7.2.1 漫反射现象

漫反射是指光线照射到粗糙表面时，光线会向各个方向均匀散射的现象。与镜面反射不同，漫反射不依赖于观察者的视角，因此漫反射光的强度只与光线入射方向和表面法线方向有关。

7.2.2 Lambert 定律

Lambert 光照模型基于 Lambert 余弦定律，该定律描述了光线在漫反射表面的强度分布。Lambert 余弦定律的数学表达式为：
$$I=I_0\cdot \cos (\theta )$$
其中：

• $I$ 是反射光的强度。
• $I_0$ 是入射光的强度。
• $\theta$ 是光线入射方向与表面法线方向的夹角。

当 $\theta =0$ 时，光线垂直于表面，反射光强度最大；当 $\theta =90^{\circ }$ 时，光线与表面平行，反射光强度为 0。

---

7.3 Lambert 光照模型的数学实现

7.3.1 点积与夹角

在 Shader 编程中，我们通常使用 点积 来计算两个向量之间的夹角。对于单位向量 $\mathbf{L}$（光线方向）和 $\mathbf{N}$（表面法线方向），它们的点积为：

$$\mathbf{L}\cdot \mathbf{N}=\cos (\theta )$$

因此，Lambert 光照模型可以简化为：

$$I=I_0\cdot (\mathbf{L}\cdot \mathbf{N})$$

7.3.2 实现漫反射强度

在 Shader 中，我们可以通过以下代码计算漫反射强度：

float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);  // 光源方向
float3 normal = normalize(i.worldNormal);              // 法线方向
float diff = max(dot(normal, lightDir), 0);            // 漫反射强度

• lightDir 是光源方向的单位向量。
• normal 是表面法线方向的单位向量。
• dot(normal, lightDir) 计算法线与光源方向的点积。
• max(..., 0) 确保漫反射强度非负。

7.3.3 结合颜色与光照

漫反射强度计算完成后，我们可以将其与物体颜色结合，得到最终的光照效果：

fixed4 col = tex2D(_MainTex, i.uv) * _Color * diff;  // 最终颜色

• tex2D(_MainTex, i.uv) 对纹理进行采样。
• _Color 是物体的基础颜色。
• diff 是漫反射强度。

---

7.4 Lambert 光照模型的局限性

虽然 Lambert 光照模型简单易用，但它也存在一些局限性：

1. 缺乏高光反射：Lambert 模型只模拟了漫反射，无法表现镜面高光效果。
2. 忽略环境光：Lambert 模型没有考虑环境光的影响，可能导致暗部过于黑暗。
3. 无法模拟复杂材质：Lambert 模型适用于粗糙表面，但不适用于金属、玻璃等复杂材质。

---