多元线性回归模型

社会经济现象的变化往往受到多个因素的影响，因此，一般要进行多元回归分析，我们把包括两个或两个以上自变量的回归称为多元线性回归 [1]。

多元线性回归的基本原理和基本计算过程与一元线性回归相同，但由于自变量个数多，计算相当麻烦，一般在实际中应用时都要借助统计软件。这里只介绍多元线性回归的一些基本问题。

但由于各个自变量的单位可能不一样，比如说一个消费水平的关系式中，工资水平、受教育程度、职业、地区、家庭负担等等因素都会影响到消费水平，而这些影响因素（自变量）的单位显然是不同的，因此自变量前系数的大小并不能说明该因素的重要程度，更简单地来说，同样工资收入，如果用元为单位就比用百元为单位所得的回归系数要小，但是工资水平对消费的影响程度并没有变，所以得想办法将各个自变量化到统一的单位上来。前面学到的标准分就有这个功能，具体到这里来说，就是将所有变量包括因变量都先转化为标准分，再进行线性回归，此时得到的回归系数就能反映对应自变量的重要程度。这时的回归方程称为标准回归方程，回归系数称为标准回归系数，表示如下：

Y=β_0+β_1X_1+ β_2X_2+ … + β_mX_m+e

由于都化成了标准分，所以就不再有常数项 a 了，因为各自变量都取平均水平时，因变量也应该取平均水平，而平均水平正好对应标准分 0 ，当等式两端的变量都取 0 时，常数项也就为 0 了。

多元线性回归与一元线性回归类似，可以用最小二乘法估计模型参数，也需对模型及模型参数进行统计检验 [2]。

选择合适的自变量是正确进行多元回归预测的前提之一，多元回归模型自变量的选择可以利用变量之间的相关矩阵来解决。

多元线性回归方程：

多元线性回归方程的建立：

下面我们用实例来看一下

数据说明：

Serial No.  序列号

GRE Score  GRE成绩

TOEFL Score  托福成绩

University Rating  大学排名

SOP  个人自述文得分

LOR  推荐信得分

CGPA  累计平均绩点

Research  发表研究论文篇数

Chance of Admit  申请成功概率

实例：

引入所需要的库：

import pandas as pd  # 导入Pandas库，用于数据处理
import numpy as np  # 导入NumPy库，用于数值计算
import seaborn as sns  # 导入Seaborn库，用于绘图
import matplotlib.pyplot as plt  # 导入Matplotlib库，用于绘图
from sklearn.model_selection import train_test_split  # 导入训练集和测试集划分函数
from sklearn.linear_model import LinearRegression  # 导入线性回归模型
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error  # 导入评估指标

读取数据：

#使用pandas库读取CSV文件
# 显示数据的前5行
data = pd.read_csv('C:/Users/dhy/Desktop/shuju/Admission_Predict.csv',engine='python')
data.head(5)

查看数据：

# 数据预处理
# 查看数据的基本信息，包括列名、非空值数量、数据类型等
data.info()

计算数据的描述性统计：

# 计算数据的描述性统计，包括均值、标准差、最小值、最大值等
data.describe()

检查数据中是否存在缺失值：

data.isnull().sum()

                        可以看出没有缺失值，如果有缺失值需要先处理缺失值。

数据可视化：

# 绘制各特征的直方图，以便观察数据分布
data.hist(figsize=(12, 10))
plt.show()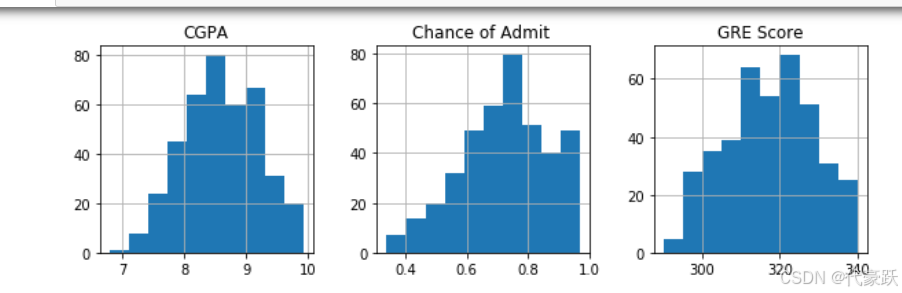

绘制热力图：

# 绘制相关系数矩阵的热力图，以了解各特征之间的相关性
corr_matrix = data.corr()
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show()

#GRE Score 和 Chance of Admit：相关系数为 0.8，表示 GRE 成绩与录取概率之间存在较强的正相关性。
#TOEFL Score 和 Chance of Admit：相关系数为 0.79，表示 TOEFL 成绩与录取概率之间也存在较强的正相关性。
#CGPA 和 Chance of Admit：相关系数为 0.87，表示 CGPA 与录取概率之间存在较强的正相关性。
#Research 和 Chance of Admit：相关系数为 0.55，表示有无研究经验与录取概率之间存在中等的正相关性。
#SOP 和 LOR：相关系数为 0.73，表示 SOP 和 LOR 之间存在中等的正相关性。

构建模型：

# 定义特征变量X（去掉序列号和目标变量）
X = data.drop(['Serial No.', 'Chance of Admit '], axis=1)
# 定义目标变量y
y = data['Chance of Admit ']

切分：

# 将数据集划分为训练集和测试集，测试集占20%
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

应用逻辑回归:

创建线性回归模型对象

model = LinearRegression()

使用训练集数据训练模型：

y_pred = model.predict(X_test)

评估模型性能：

# 计算均方误差（Mean Squared Error），用于衡量预测值与实际值之间的平均平方差异
mse = mean_squared_error(y_test, y_pred)
print（mse）

#平均绝对误差（MAE）
mae = mean_absolute_error(y_test, y_pred)
print（mae）

# 计算决定系数R²，用于衡量模型解释的数据变异性的比例
r2 = r2_score(y_test, y_pred)
print（r2）

mse=0.0046170033772850085
mae=0.047956733620912
r2=0.8212082591486992

# 如果MSE较小，说明模型的预测误差相对较低

#同样是一个较小的值，进一步确认了模型的预测误差较小。

# R²接近于1，说明模型具有很好的预测能力

画图：

可视化预测结果与实际结果的对比

#使用 scatter 方法绘制实际值与预测值的散点图，以便直观地比较模型的预测效果。
plt.scatter(y_test, y_pred)
plt.xlabel('Actual Chance of Admit')
plt.ylabel('Predicted Chance of Admit')
plt.title('Actual vs Predicted Chance of Admit')
plt.plot([0, 1], [0, 1], color='red', linestyle='--')
plt.show()

#MSE 值为 0.0046非常小的值，表明模型的预测误差很小，模型对数据的拟合度较高。
#MAE 值为 0.047956733620911955，同样是一个较小的值，进一步确认了模型的预测误差较小。
#R²接近于1，说明模型具有很好的预测能力

#大多数点都集中在线附近，表明模型的预测值与实际值非常接近，验证了模型的良好性能

总结：

1. 导入必要的库：

   • pandas：用于数据处理。
   • numpy：用于数值计算。
   • seaborn 和 matplotlib：用于绘图。
   • train_test_split：用于划分训练集和测试集。
   • LinearRegression：用于创建线性回归模型。
   • mean_squared_error、r2_score 和 mean_absolute_error：用于评估模型性能。

2. 加载数据：

   • 使用 pd.read_csv 函数读取 CSV 文件，指定分隔符为逗号。
   • 使用 head() 方法输出数据的前几行，以便快速查看数据格式。

3. 数据预处理：

   • 使用 info() 方法输出数据的基本信息，包括列名、非空值数量、数据类型等。
   • 使用 describe() 方法输出数据的描述性统计，包括均值、标准差、最小值、最大值等。
   • 使用 isnull().sum() 方法检查数据中是否存在缺失值。

4. 数据可视化：

   • 使用 hist() 方法绘制各特征的直方图，以便观察数据分布。
   • 使用 corr() 方法计算相关系数矩阵，并用 seaborn 库的 heatmap 函数绘制热力图，以了解各特征之间的相关性。

5. 构建模型：

   • 定义特征变量 X，去掉序列号和目标变量 Chance of Admit。
   • 定义目标变量 y 为录取概率。
   • 使用 train_test_split 函数将数据集划分为训练集和测试集，测试集占20%。
   • 创建线性回归模型对象 LinearRegression。
   • 使用训练集数据训练模型。
   • 使用测试集数据进行预测。

6. 评估模型性能：

   • 计算均方误差（MSE），用于衡量预测值与实际值之间的平均平方差异。
   • 计算平均绝对误差（MAE），用于衡量预测值与实际值之间的平均绝对差异。
   • 计算决定系数 R²，用于衡量模型解释的数据变异性的比例。
   • 输出评估指标。

7. 可视化预测结果与实际结果的对比：

   • 使用 scatter 方法绘制实际值与预测值的散点图，以便直观地评估模型的预测效果。
   • 绘制对角线，以便直观地比较模型的预测值与实际值。