系统简介

本文利用Poisson回归模型和统计软件SPSSAU通过分析数据来研究如何降低交通事故伤亡率。
近几年来，威胁着人们生命安全的重要因素之一是交通事故，其中交通事故的发生存在着很多因素。为了降低交通事故伤亡率，急需找寻方法来明确影响交通事故伤亡率的相关因素。Poisson回归模型是一类广义线性回归模型，通过分析因变量来计数数据，并且在医学、生活安全等很多研究领域有着重要应用。本论文在介绍泊松回归模型原理和方法的基础上，进一步研究Poisson回归模型在分析交通事故伤亡率上的应用。收集某地区交通事故的统计数据，利用Poisson回归模型探究影响交通事故伤亡率的主要因素，进而提出可行性建议，以此来降低交通事故伤亡率[1]p584。

关键词 交通事故 伤亡率 Poisson回归模型 SPSS

引 言

Poisson分布模型在生活中应用十分广泛，例如，如果将一所医院中的每个病人看病的事件看做是一个随机事件，而且满足事件之间没有影响，那么就可以认为在某时间段内，这个医院所接纳病人人数是服从Poisson分布的一个随机的变量。换而言之，当一个事件发生的时间短到可以忽略不计，那么这个这个事件在这个连续的时间段内发生的次数就能用泊松分布区描述。生活中也常常能找到可以用泊松分布描述的问题，就比如说一条繁杂的街道上一段时间内通车次数、细胞从出现再到分裂等变化的一个过程等等都遵从Poisson分布。其实，Poisson分布也可以当做是二项分布的一种。二项分布本质是一种关于事件“发生”和“不发生”的分布，而当二项分布满足样本量很大并且发生概率很小的时候就是Poisson分布。因为二项分布能够用来描述很多与自然界相关的随机现象，所以作为二项分布极限形式的泊松分布也能广泛的运用在描述自然界现象和生活问题中[2]p93。
最近几年，关于Poisson回归模型的研究，取得了很大的进步。下面主要介绍所涉及到的领域以及相关的例子。
(1)医学方面
在2010年的时候高韦曾发表一篇关于用Poisson回归模型来解决新生儿缺陷问题的学位论文。在文章里就详细的介绍了一下Poisson回归模型并提出它在帮助解决医学上新生儿缺陷以及各种疾病问题所能起到的作用。考虑到不同模型参数会对数据有影响，所以他对参数的选用进行了深刻的研究与探讨，找寻出最恰当的模型参数来建立相关模型。建立模型的时候，着重分析观察每个因素对新生儿缺陷的影响力，以此来确定哪个因素对之影响最大。最后，提供必要的参考依据，提出自己对解决新生儿缺陷医学问题的观点和干预方案[3]。
2019年夏春花、王笑灵发表的《北京海淀区儿童受阻口病的发病与气象因素相关性研究》期刊中利用计算机软件对数据进行单因素与多因素的拟合分析，以此来确定发病情况所受气象因素的影响程度。改文章里主要选用了气温、气压等等几个因素。通过实验数据分析以及软件所得结果分析得住该病收诸多气象因素影响，并且存在多个影响关系，有线性相关和曲线相关，同样也有负向相关。最后得住，该病的发病率与当地的气象因素存在诸多联系。而所得结果就是用Poisson回归分析的方法得到的[4]p892。
(2)生活安全方面
2018年田野在一篇关于林火预测的学位论文中以某一地区的森林火灾、气候要素、地理样貌特征等等数据为基础以每个月和每一天为尺度建立相关的Poisson回归模型对当地的森林火灾情况进行深入研究，以此来预测该地区在未来几年内的林火发生情况。该模型为当地的森林火灾预测预报提供了科学依据,并为该区域林火管理工作有效开展提供理论参考[5]
2020年Tomoaki Nishino和Akihiko Hokugo在《基于2011年东北地震点火记录的建筑物震后火灾点火次数时间序列预测随机模型》中从2011年东北地震的点火记录中提取了126个地震动影响下的点火源，应用Poisson回归模型对2011年东北地震的点火次数进行了时间序列预测[6]p32。
2003年Wang kui和Lee Andy等人在《用二元零膨胀Poisson回归模型分析职业伤害》中提出一个二元零膨胀poisson回归模型，用以评估公立教学医院清洁服务部参与式工效学团队干预。结果显示，该回归模型提供了一个令人满意的数据拟合，并且干预与总体损伤发生率和肌肉骨骼损伤平均数的显著减少相关，而非肌肉骨骼质的损伤的减少是微不足道的。该方法可用于评估对其他职业伤害高危人群进行干预试验的有效性[7]p202。
本文主要通过Poisson回归模型来研究交通事故伤亡率的影响因素，将通过以下几个方面来研究。
第一部分：引言部分，介绍选该题的意义以及Poisson回归模型研究现状；
第二部分：正文部分，首先介绍线性回归的理论方法与原理，然后介绍Poisson分布理论，Poisson回归模型的相关知识。
第三部分：选取具体问题进行具体分析，利用软件和公式得出结果
第四部分：分析所得结果得出结论，提出合理性建议。
1.线性回归模型
1.1 线性回归模型的理论与方法
通俗的讲，线性回归分析的原理就是通过一个自变量或者一组自变量变化来预测另一个或者另一组与之相关的变量的一种分析方法。回归方程又分为两种，即为一元回归与二元回归，这主要根据它自变量的个数来判断。当回归函数是线性函数的时候，变量间就是线性相关的。一元线性回归分析包括两个变量，一个是自变量，以表示。另一个是因变量(预测变量)以表示。
基本内容：
假设与是来自样本观察值的一组已知数据，那么这组观察值应当满足如下条件：
（1） 两组观察值之间彼此相互独立，并且围绕回归线的波动服从正态分布;
（2）该组数据沿回归直线方向的方差处处相等;
（3）与属于线性相关。如果影响预测变量的主要因素不单单只有一个，则被称为多元线性回归分析。它的原理与一元回归基本相同，区别在于运算更为复杂，一般需要通过计算机来完成。
1.2 例举实例
例举一组房屋面积和价格的数据，如下图：
表1 房屋面积及相对应的价格
房屋面积 价格

50 47
70 72
88 80
69 77
100 110
120 100
130 ？
那么，给出房屋面积为130，能否根据上文已知数据来预测它的价格呢？这时候，就要用到线性回归模型了。
首先需要画出已得数据的散点图：

图1 房屋面积与价格的图示
接着来分析线性回归具体作用：根据上文散点图模拟一条直线，让数据点尽量落在直线周围，如下图：

图2 房屋面积与价格的图示
用公式表示的话，这个线性模型就是一条直线：
其中，为系数，为截距。 （1.1）

2. Poisson回归模型

2.1 Poisson分布
1838年法国数学家泊松曾发表一种离散概率分布，这就是人们今天在统计与概率学里常用到的Poisson分布。
泊松分布的适用范围非常广泛。当所求问题反映的是连续时间内事件发生次数的概率问题时，就可以用到泊松分布了。简而言之，泊松分布可以根据时间或空间上已发生事件的次数以及规律来预测该事件在同时间或空间内发生不同次数的概率。也正因为如此，它在人们日常生活中的应用十分广泛，对于处理生活中一些概率问题非常快捷与方便。
2.2 Poisson回归模型理论与方法
在统计学里，用到的回归分析方法有好几种。Poisson回归分析就是其中的一种。它主要是用来计算数据的资料和列出数据间联系建立模型的一种方法。利用它，假设反应变量符合泊松分布，并且可以用未知参数来线性表达期望值的对数。Poisson回归模型在特定的情况下也能称为对数线性模型，而它的条件就是Poisson回归被用于列表分析[8]p58。
广义线性模型有很多种，Poisson回归模型就是它的一种。当数据中的因变量满足Poisson分布的条件是，Poisson回归模型就可以表达为：
（2.1）
（2.2）

式中，是泊松分布的均值；是连接函数。
如果随机变量服从参数为的泊松分布，则其概率函数可以表示为:
，=0,1,2,… （2.3）

2.2.1模型设定
指数分布族的密度函数可以表示为下面的一般形式:
（2.4）

对式(2.4)变形，泊松分布的概率函数也可以表示为指数分布族的形式，即
（2.5）

对比式(2.4) 和式(2.5)，有
（2.6）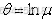
（2.7）

泊松回归模型的一般形式可以表示为:
（2.8）

（2.9）

式中，表示连接函数；为线性预测项。
在广义线性模型中，正则连接函数是使得成立的函数。在泊松分布假设下，所以相应的正则连接函数就是对数连接函数，即。
平均每个车年的索赔次数，即索赔频率[10]。

3．数据分析

3.1 提出问题
为研究某市道路交通事故伤亡率的影响因素，本文收集了某市2019年全年道路上责任人车型、驾驶人驾龄和性别等作为样本。整体来看各组变量组内与组间皆存在不同程度的差异，因而可以粗略估计出变量与分类对交通事故伤亡率影响程度各不相同，根据当地交警支队发布的数据统计结果如下：
表2 某市2019年全年交通事故分类统计表
变量 分类 交通事故/起 占比
责任人车型（0） 小型客车 314 47.70%
摩托车 73 10.98%
电动自行车 71 10.91%
驾驶人驾龄（1） 6-10年 136 20.67%
11-15年 96 14.57%
20年以上 62 9.46%
驾驶员性别（2） 男性 561 85.06%
女性 98 14.94%
事故原因（3） 未按规定让行 102 15.40%
违反交通信号 49 7.43%
超速行驶 32 4.83%
时间（4） 6:00-9:00 110 16.76%
15:00-18:00 120 18.22%
18:00-21:00 111 16.81%
人群分类（5） 农民 211 31.97%
工人 142 21.62%
自主经营者 104 15.71%

问题分析：根据表二可知该市的2019年全年交通事故中当研究变量是责任人车型时小型客车发生的交通事故数所占比重数较大。因此，对于驾驶小型客车的司机交警应重点教育与监督。而其他两种车虽占比重较小但也不容小觑，要做到认真驾驶，安全驾驶；当变量为驾驶人驾龄时根据图表可知驾龄较小的易发生交通事故，所以对于一些驾驶技术较弱驾龄较小的人要多加督促与引导，自身也应该主动学习交通安全驾驶相关知识；驾驶员性别来看，男司机所占比重明显高于女司机；从主要原因来分析可知交通规则对于交通道路安全影响非常之大，因此司机要熟练掌握交通规则，遵守交通法规；从时间来看，每天交通事故发生存在高峰期，司机要多多注意。
3.2 结果分析
利用SPSS软件建立Poisson回归模型对上文问题分析。步骤：导入数据，打开左侧实验/医学研究一栏选择Poisson回归将变量，分类拉到右侧X一栏中，交通事故拉到Y一栏。如下图：

图3 运用SPSS软件进行
SPSS输出结果如下：
表3 Poisson回归模型似然比检验结果
似然比卡方值 df p AIC 值 BIC 值
573.696 2 0.000 853.235 855.735
此表格用于模型检验，此处放入两个X变量分别为：变量、分类。并且P值为0.000<0.05,说明放入两个自变量以后，模型质量有很大的提升，那么就可以证明构建该模型是有实际意义的。表中的似然比卡方值和df值可以不予考虑。但AIC值和BIC值用于多次分析对比，来优化模型，所以越低越好。
表4 Poisson回归分析结果汇总 (n=17)
项 回归系数 标准误 z 值 p 值 OR值 OR值95% CI(LL) OR值95% CI(UL)
变量 -0.028 0.012 -2.380 0.017 0.972 0.950 0.995
分类 -0.647 0.029 -22.512 0.000 0.524 0.495 0.554
截距 6.143 0.057 108.308 0.000 465.593 416.606 520.341
因变量: 交通事故
McFadden R 方: 0.404
从上表可知，将变量, 分类共2项为自变量，这里的因变量则是交通事故的起数。对此进行Poisson回归分析。再次观察表格可知，模型伪R方的值为0.404。由此说明两个自变量能解释因变量即交通事故的起数40.4%的变化原因。故可以得到所求模型公式：
（3.1）

最终具体分析可知：
变量的回归系数为-0.028，并且呈现出0.05水平的显著性(z=-2.380，p=0.017<0.05)。因此能够得到变量对交通事故伤亡率有负向影响。观察上表还可得出优势比为0.972，说明当变量增加一个单位时，交通事故的起数减少幅度为0.972倍。
分类的回归系数为-0.647，并且呈现出0.01水平的显著性(z=-22.512，p=0.000<0.01)。故而说明分类对交通事故伤亡率有显著的负向影响。再由优势比为0.524，可得分类每增加一个单位时，交通事故的起数减少幅度为0.524倍。
总结分析结果可得：变量, 分类共2项全部均会对交通事故产生显著的负向影响关系。

结 论

结合数据和SPSS软件分析结果可知：
（1）结果分析检验可得变量以及分类对交通事故伤亡率皆有影响；
（2）变量与分类对交通事故伤亡率都存在负向影响关系且变量影响关系更大一些；
（3）客观数据来看，小型客车同组间差异较大，男性驾驶员占比明显高于女性驾驶员；
（4）驾龄时间越长的事故发生率越少，分类中农民交通安全意识较低，因而占比较大。
（5）时间对交通事故伤亡率无影响，各时间段差异较小；
基于以上讨论，给出如下建议：
（1）提高驾照考核难度，严格执行相关法律法规，对于未达标准学员坚决不予驾驶权利；
（2）加强小型客车管控力度，对违章行为加大处罚力度；
（3）相关部门应多设立执法观察点，对未按规定让行行为进行教育批评与处罚，加强对人民的素质教育。
（4）加强对农民和工人的交通安全意识以及交通法律法规相关知识教育与监督；
（5）重点督促与引导男性司机正确的交通安全意识，培养正确的驾驶习惯。