人智导(六):“不可测”问题的求解
人智导(六):“不可测”问题的求解动作效果的不确定性如图所示:智能体不能确切地直到其动作的效果,可能有多个结果状态表示为:[s1,…,sn]=result(s0,a)[s_1,\dots ,s_n]=result(s_0,a)[s1,…,sn]=result(s0,a)动作效果不确定,需要与环境交互在执行动作之前,智能体需要计算所用结果状态的概率P(si∣a)P(s_i|a)P(si∣a)
人智导(六):“不可测”问题的求解
动作效果的不确定性
如图所示: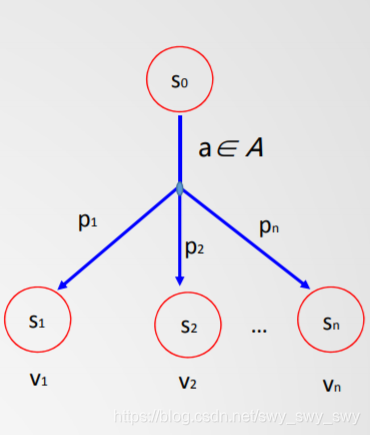
- 智能体不能确切地直到其动作的效果,可能有多个结果状态
- 表示为:[s1,…,sn]=result(s0,a)[s_1,\dots ,s_n]=result(s_0,a)[s1,…,sn]=result(s0,a)
- 动作效果不确定,需要与环境交互
- 在执行动作之前,智能体需要计算所用结果状态的概率P(si∣a)P(s_i|a)P(si∣a)
- 动作的期望效用(Expected Utility):EU(a)=ΣiP(si∣a)V(si)EU(a)=\Sigma_iP(s_i|a)V(s_i)EU(a)=ΣiP(si∣a)V(si)
- 状态价值函数V(s)V(s)V(s):状态到实数值的映射
- 智能体应当选择当前状态下具有最大期望效用(MEU)的动作
最优策略
- 动作后续状态确定(deterministic)的搜索问题
- 发现最优(optimal)plan,从初始状态到目标状态的一个动作序列
- 动作后续状态不确定(nondeterministic)
- 发现一个最优(optimal)policy π∗:s→a\pi ^* :s\to aπ∗:s→a
- policy策略为一个状态确定应采取的动作(what to do)
- 最优的policy是满足MEU的
不确定条件下的搜索问题
如图: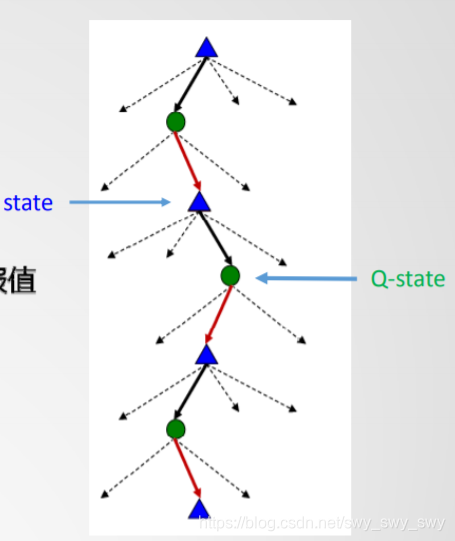
- “不可测”问题
- 目标导向(goal-seeking)
- 与环境交互,只有动作执行后才能确定后续状态
- 趋向目标的累计回报(reward),而非动作直接的回报值
- 求解方法
- 发现最优policy策略π∗:s→a\pi ^*: s\to aπ∗:s→a
- 即在任何一个状态sss,确定趋向目标的最佳动作aaa
- 定义Q-state状态表示(计算)EU
与环境交互模型
如图: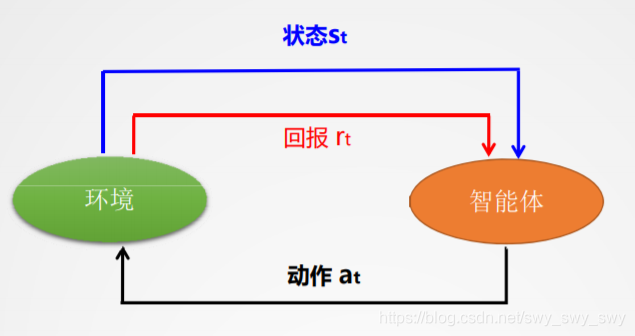
定义三个本体元素:
状态(state)、动作(action)、回报(reward)
智能体所面对的问题:
与环境交互中确定动作的后续状态,达到目标
马尔可夫决策过程
马尔可夫决策过程(Markov Decision Process):
- 一个状态(state)集合:SSS
- 一个动作(actions)集合:AAA
- 一个后继函数T(s,a,s′)T(s,a,s')T(s,a,s′),且从状态sss到s′s's′的概率为P(s′∣s,a)P(s'|s,a)P(s′∣s,a)
- 一个回报(reward)函数:R(s,a,s′)R(s,a,s')R(s,a,s′)
- 初始状态s0s_0s0
- 一个或多个目标(结束)状态
马尔可夫过程
基本性质
无记忆性(memoryless)
动作和后继状态仅取决于当前所在状态,与之前的状态无关
P(St+1=s′∣St=st,At=at,St−1=st−1,At−1,…,S0=s0)=P(St+1=s′∣St=st,At=at)P(S_{t+1}=s'|S_t=s_t, A_t=a_t,S_{t-1}=s_{t-1},A_{t-1},\dots ,S_0=s_0)=P(S_{t+1}=s'|S_t=s_t,A_t=a_t)P(St+1=s′∣St=st,At=at,St−1=st−1,At−1,…,S0=s0)=P(St+1=s′∣St=st,At=at)
正如标准搜索模型,后续函数仅依赖于当前状态
Markov搜索树
如图: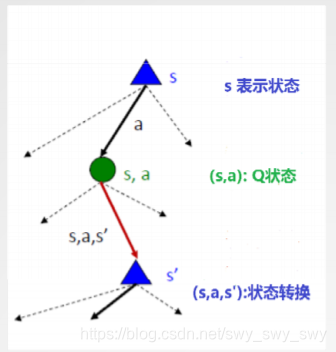
MDP:求解动作效果不确定问题
- 对任意状态sss下的动作选择:policy π∗(s):s→apolicy~\pi^*(s):s\to apolicy π∗(s):s→a
- 任意状态sss选这样的动作,使得价值函数V(s)V(s)V(s)计算累计回报(sum of rewards)期望最大化
如何选择最优动作
- 对任意一个状态sss,都通过价值函数对应一个值
- V(s)=V(s)=V(s)=累计回报最大期望值{目标状态VVV值为0}
- 最优策略:π∗=argπ max Vπ(s),(∀s)\pi ^* =arg_{\pi}~max~V^{\pi}(s),(\forall s)π∗=argπ max Vπ(s),(∀s)
示例: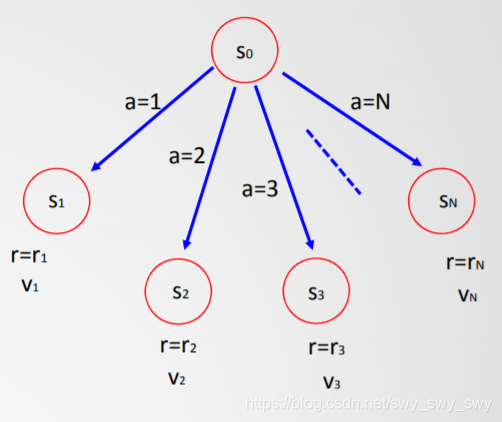
如上图
V0=maxa∈1,…,N(ra+γVa)V_0=max_{a\in 1, \dots ,N}(r_a+\gamma V_a)V0=maxa∈1,…,N(ra+γVa)
- 非确定动作的最大期望值(如下图)V0=maxa∈AΣs∈SPa,s0→s(rs+γVs)V_0=max_{a\in A}\Sigma _{s\in S}P_{a, s_0\to s}(r_s+\gamma V_s)V0=maxa∈AΣs∈SPa,s0→s(rs+γVs)
- 同时体现了当前动作对后续进程的影响Vπ(st)=rt+γrt+1+γ2rt+2+⋯=Σi=0∞γirt+iV^{\pi}(s_t)=r_t +\gamma r_{t+1} +\gamma^2r_{t+2}+\dots =\Sigma^{\infty}_{i=0}\gamma ^i r_{t+i}Vπ(st)=rt+γrt+1+γ2rt+2+⋯=Σi=0∞γirt+i
引入Q(s,a)Q(s,a)Q(s,a)状态表示
- 状态sss及其状态值:V(s)=V(s)=V(s)=始于sss按最优策略行动的累计回报
- Q(s,a)Q(s,a)Q(s,a)的值:Q(s,a)=EU(a)Q(s,a)=EU(a)Q(s,a)=EU(a),在sss状态下执行aaa
- 最优策略policy:π∗(s)\pi ^* (s)π∗(s) π∗=argπmax V∣pi(s),(∀s)\pi ^*=arg_{\pi}max~V^{|pi}(s),(\forall s)π∗=argπmax V∣pi(s),(∀s)
最优策略的计算
- 有如下等式(0≤γ≤1)(0\le \gamma\le 1)(0≤γ≤1): V(s)=maxa Q(s,a)V(s)=max_a ~Q(s,a)V(s)=maxa Q(s,a) Q(s,a)=Σs′P(s,a,s′)[r(s,a,s′)+γV(s′)]Q(s,a)=\Sigma_{s'}P(s,a,s')[r(s,a,s')+\gamma V(s')]Q(s,a)=Σs′P(s,a,s′)[r(s,a,s′)+γV(s′)] (Bellman equation) V(s)=maxaΣs′P(s,s,s′)[r(s,a,s′)+γV(s′)](Bellman~equation)~V(s)=max_a\Sigma_{s'}P(s,s,s')[r(s,a,s')+\gamma V(s')](Bellman equation) V(s)=maxaΣs′P(s,s,s′)[r(s,a,s′)+γV(s′)]
- 迭代计算:Vk+1(s)←maxaΣs′P(s,a,s′)[r(s,a,s′)+γVk(s′)]V_{k+1}(s) \leftarrow max_a\Sigma_{s'}P(s,a,s')[r(s,a,s')+\gamma V_k(s')]Vk+1(s)←maxaΣs′P(s,a,s′)[r(s,a,s′)+γVk(s′)]
状态值迭代计算方法: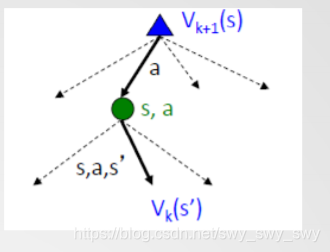
状态空间:
S={s1,…,sn} S=\{s_1, \dots ,s_n\}S={s1,…,sn}
Bellman方程组(每个状态对应一个方程):
[Vs1⋮Vsn]=[P11⋯P1n⋮⋱⋮Pn1⋯Pnn][Vs1⋮Vsn] \left[ \begin{matrix} V_{s1}\\ \vdots \\ V_{sn} \end{matrix} \right] = \left[ \begin{matrix} P_{11} &\cdots &P_{1n}\\ \vdots &\ddots &\vdots \\ P_{n1} &\cdots &P_{nn} \end{matrix} \right] \left[ \begin{matrix} V_{s1}\\ \vdots \\ V_{sn} \end{matrix} \right] ⎣⎢⎡Vs1⋮Vsn⎦⎥⎤=⎣⎢⎡P11⋮Pn1⋯⋱⋯P1n⋮Pnn⎦⎥⎤⎣⎢⎡Vs1⋮Vsn⎦⎥⎤
其中:
Pij={pi→jif j∈successor(i)0otherwiseP_{ij}=\begin{cases}p_{i\to j} &if~j\in successor(i) \\ 0 & otherwise \end{cases}Pij={pi→j0if j∈successor(i)otherwise
向量表示:
Vk+1=PVkV_{k+1} = PV_kVk+1=PVk
初始条件:
V0=[0⋮0]V_0=\left[\begin{matrix}0\\ \vdots \\0 \end{matrix}\right]V0=⎣⎢⎡0⋮0⎦⎥⎤
举例
问题: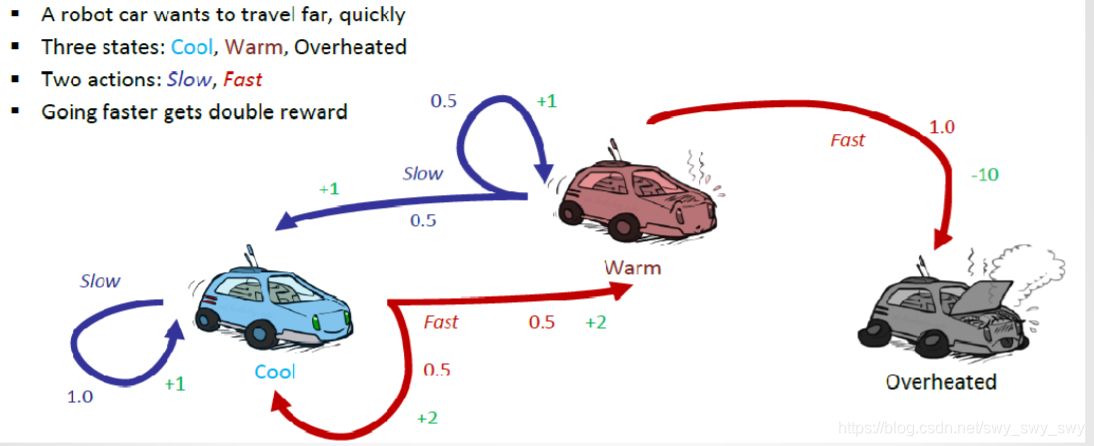
MDP搜索树: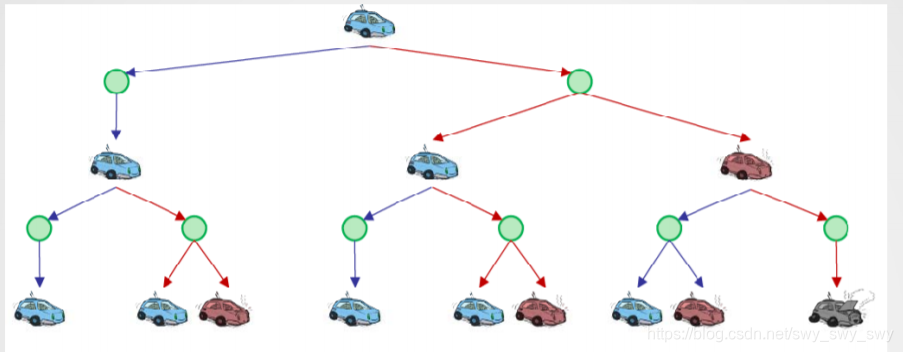
迭代计算: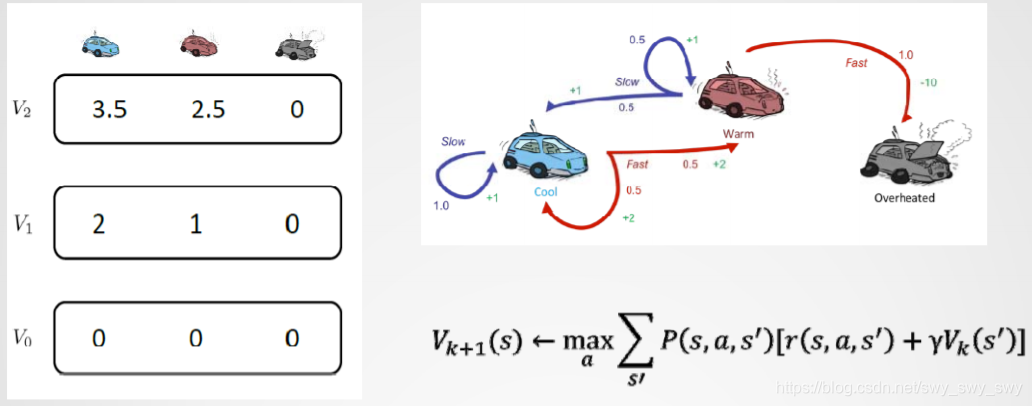
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)