人智导（八）：模型的评价

均方误差估计

针对回归模型，最常用的为均方误差估计(Mean Squarred Error)
$$MSE=\frac{1}{n}{\Sigma }_{i=1}^n(f_{\beta }^{\prime }(x_i)-y_i{)}^2$$

• 模型评价：expected lowest testing MSE
• 注意学习模型的估算参数$\beta$是lowest training MSE
• 模型需要在方差(variance)与偏差(bias)之间平衡

偏差与方差

二者的平衡

• 模型方差大，方法自由度就高，趋于非线性，拟合训练数据好（偏差小）
• 偏差大且模型方差小（趋于线性），训练精度相对低，但测试集上泛化能力强
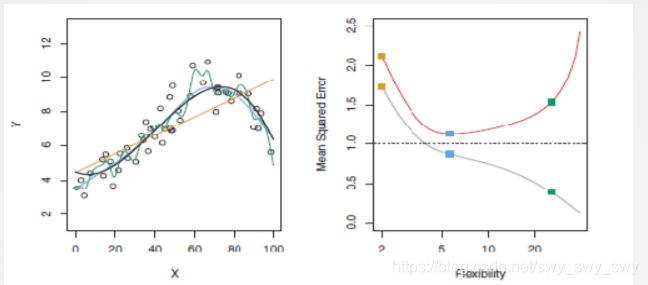
• 理想的学习方法：低方差，低偏差（$f$形式变化尽可能少）
• 如图，左图中黑线是真实的$f$，右图金黄线是training情况，右图灰色线是testing情况
  

图解偏差与方差
如图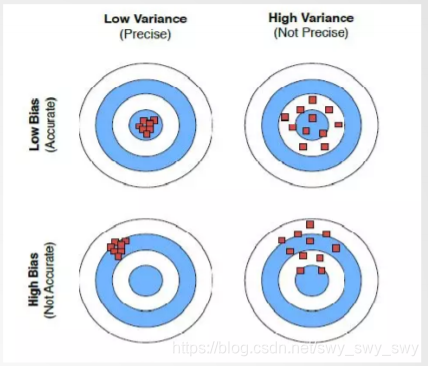

• 期望的学习方法：低偏差，低方差（左上图）
• 偏差：准确度（点集质心距离靶心越近越好）（右上图）
• 方差：精度（点越密越好）（左下图）

模型评估：顶层设计

• 构建回归模型：training MSE（乐观估计）
• 模型性能评价：test MSE（悲观估计）
• 建模的目标：expected test MSE 最小化，即最小化$$E(y_0-\hat{f}(x_0){)}^2=Var(\hat{f}(x_0))+[Bias(\hat{f}(x_0)){]}^2$$ 其中$x_0$表示一组测试数据

验证集方法

• 验证集方法(holdout 方法)
  • 样例数据划分为不交叠两部分：
  • 训练集生成模型，验证集做测试评估
  • 在验证集上评估模型对未知数据预测的泛化能力
• 验证集方法带来的问题
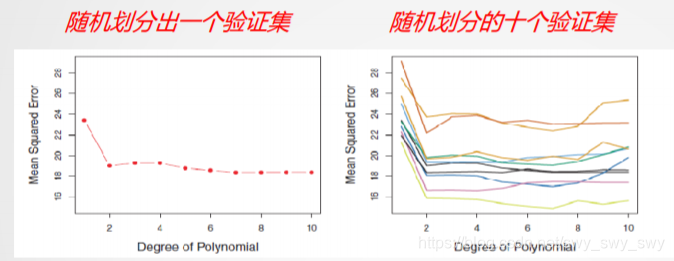
  • 不确定性：不同的验证集可能给出的test MSE结果是非常不同的
  • 在验证集上评价test MSE是悲观估计，用尽可能多的样例参与模型性能训练会更好
• 验证集方法：一般是样例数据集规模较大的情况下使用

重复holdout验证

• 多次随机划分训练集和验证集，重复holdout方法评估模型取平均值，更鲁棒
• 亦成为蒙特卡洛(Monte Carlo)交叉验证

留一交叉验证

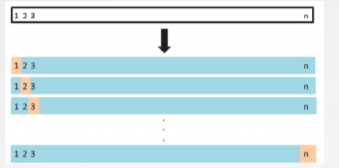
留一(leave-one-out)交叉验证方法：
数据集包括n个样例，选一份做验证，其它n-1份为训练集，重复n次
非常高的计算代价（若n很大），评估一个学习算法需要生成模型n次，取平均的test MSE
$$LOOC{V}_{(n)}=\frac{1}{n}{\Sigma }_{i=1}^{n}MS{E}_i$$
适用于样例集较小情况，充分利用训练数据进行模型评估的方法

K-折交叉验证方法

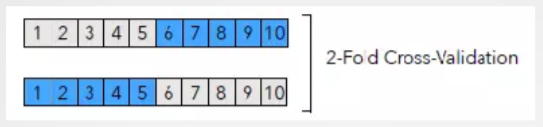
数据集等分为k份，选一份做验证，其它k-1份为训练集，重复k次
较高的计算代价，评估一个学习算法需要k次生成模型，取平均的test MSE
$$C{V}_{(k)}=\frac{1}{k}{\Sigma }_{i=1}^{k}MS{E}_i$$
K-折交叉验证较理想地折中考虑偏差与方差情况

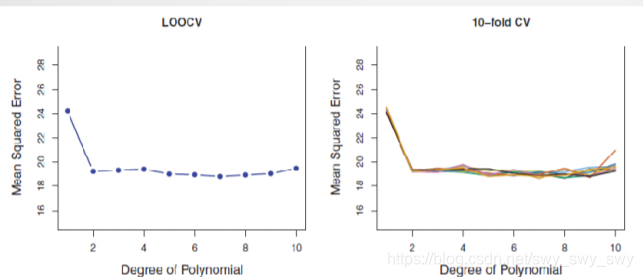
留一与K-折交叉验证效果

如图