灰色预测的主要特点是模型使用的不是原始数据序列,而是生成的数据序列。其核
心体系是灰色模型(Grey Model,GM),即对原始数据作累加生成(或其他方法生成)得到
近似的指数规律再进行建模的方法。优点是不需要很多的数据,一般只需要4个数据,就
能解决历史数据少、序列的完整性及可靠性低的问题;能利用微分方程来充分挖掘系统的
本质,精度高;能将无规律的原始数据进行生成得到规律性较强的生成序列,运算简便,易
于检验,不考虑分布规律,不考虑变化趋势。缺点是只适用于中短期的预测,只适合指数
增长的预测。

GM(1，1)模型的定义

例题：，请根据下面数据预测1993年到2022年的道路交通噪声平均声级

数据的检验与处理

数据的生成

原始数据

x0 <- c(71.1,72.4,72.4,72.1,71.4,72.0,71.6);x0

级比检验

代码：

# 级比检验
test <- function(lamda){
  n <- length(x0)
  lamda=x0[1:(n-1)]/x0[2:n]
  min <- min(lamda)
  max <- max(lamda)
  if(exp(-2/(n+1))<min){
    if(max<exp(2/(n+2))){
      print("可直接预测")}
  }
  else{
    print("需做变换")
  }  
}
test(lamda)

故可以使用x0作令人满意的GM(1,1)模型

GM(1,1)建模

生成累加数据和均值数据

#累加数据
x1 <- cumsum(x0);x1
# 均值数据
z1 <- c()
n=length(x0)
for ( i in 2:n)
  z1[i-1] <- -(0.5*x1[i]+0.5*x1[i-1])
z1

构造矩阵$B$及数据向量$Y$,有

# 构造矩阵B
one <- gl(1,6);one
B1<- c(z1,one);B1
B <-array(B1,dim=c(6,2));B
#构造Y
Y=x0[-1];Y

计算：

这里需要计算${\left(B^{T}B\right)}^{-1}{B}^{T}Y$,R语言矩阵的相关计算可以看我的这篇文章
crossprod(B,B)计算$B^{T}B$， solve(crossprod(B,B))计算${\left(B^{T}B\right)}^{-1}$，
%*%表示两个矩阵的乘积，solve(crossprod(B,B))%*%crossprod(B,Y)计算${\left(B^{T}B\right)}^{-1}{B}^{T}Y$

u<- solve(crossprod(B,B))%*%crossprod(B,Y);u

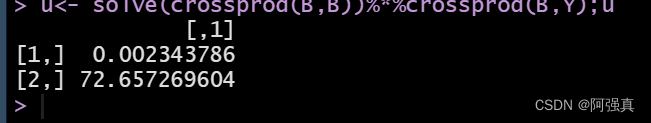
提取u里面的a和b

# 提取u里面的a和b
a <- u[1];a
b <- u[2];b

建立模型，求解，并还原数据

求解x1（累加数据值）

# 模型求解
pre <- c()
for (i in 0:16)
  pre[i+1] <- (x0[1]-b/a)*exp(-a*i)+b/a
pre

数据还原，预测值的求解

pre1 <- c()
pre1[1] <- x0[1]
for (i in 2:15)
pre1[i] <- pre[i]-pre[i-1]
pre1
time <-c(1986:(1986+length(pre1)-1))
time
x0=c(x0,rep(NA,length(pre1)-length(x0)))

模型检验

生成时间序列图

time <-c(1986:(1986+length(pre1)-1))
x0=c(x0,rep(NA,length(pre1)-length(x0)))
##注意这里为了保持预测值和原始值的数量一致，怎么一致呢就是给原始值后面加上一些空值，同是年份的长度也保持一致
data <- data.frame(time,pre1,x0);data
library(tidyverse)
library(reshape2)
mydata<-melt(data,id="time");mydata
colnames(mydata)<-c("year","sample","value")
ggplot(mydata,aes(x=year,y=value,group=sample,shape=sample,col=sample))+geom_line()+
  geom_point(size=3)+xlab("年份")+ylab("噪声")+
  scale_x_continuous(breaks =seq(1986,2020,2) )+
  scale_y_continuous(limits = c(70,73))+
  theme(legend.position = c(0.05,0.915),legend.box.background=element_rect(color="black"),
        axis.title.y=element_text(size = 14,color=4))

看起来误差很大，实际上是因为坐标轴的刻度范围很小，预测效果还是可以的

从图片上可以看出数据拟合较好
可以做进一步的检验：

计算残差，相对误差，级比偏差

最后用DT包的datatable函数展示我们的表格

#进一步检验
year <- 1986:1992
x0 <- c(71.1,72.4,72.4,72.1,71.4,72.0,71.6);x0
predict <- round(pre1[1:7],3)
res <-round(x0-predict,4) #计算残差，保留四位小数
error <- round(abs(res/x0),4)#计算相对误差，保留四位小数
lamda=round(x0[1:(n-1)]/x0[2:n],3)#计算级比偏差
perror <-round(1-(1-0.5*a)/(1+0.5*a)*lamda,3) 
perror <- append(NA,perror)
blank <- data.frame(year,x0,predict,res,error,perror)
colnames(blank) <- c("年份","原始值","预测值","残差","相对误差","级比偏差")
library(DT)
datatable(blank)