最近两次遇到关于信用卡评分的题目，遂了解一波。

Reference: 

基于python的信用卡评分模型(超详细！！！)

https://www.jianshu.com/p/f931a4df202c

https://blog.csdn.net/zs15321583801/article/details/81234446

https://blog.csdn.net/han_xiaoyang/article/details/52788775

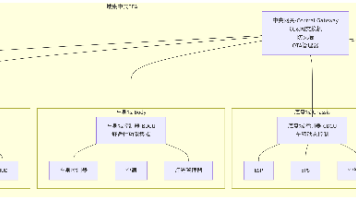
信用风险计量体系包括主体评级模型和债项评级两部分。主体评级和债项评级均有一系列评级模型组成，其中主体评级模型可用“四张卡”来表示，分别是A卡、B卡、C卡和F卡；债项评级模型通常按照主体的融资用途，分为企业融资模型、现金流融资模型和项目融资模型等。 我们主要讨论主体评级模型的开发过程。

一、项目流程

典型的信用评分模型如图1-1所示。信用风险评级模型的主要开发流程如下：
（1） 数据获取，包括获取存量客户及潜在客户的数据。存量客户是指已经在证券公司开展相关融资类业务的客户，包括个人客户和机构客户；潜在客户是指未来拟在证券公司开展相关融资类业务的客户，主要包括机构客户，这也是解决证券业样本较少的常用方法，这些潜在机构客户包括上市公司、公开发行债券的发债主体、新三板上市公司、区域股权交易中心挂牌公司、非标融资机构等。【针对存量客户数据、潜在客户数据】
（2） 数据预处理，主要工作包括数据清洗、缺失值处理、异常值处理，主要是为了将获取的原始数据转化为可用作模型开发的格式化数据。【数据清洗 + 缺失值处理 + 异常值处理】
（3） 探索性数据分析，该步骤主要是获取样本总体的大概情况，描述样本总体情况的指标主要有直方图、箱形图等。【变量分布情况 + 中位数 + 均值 】
（4） 变量选择，该步骤主要是通过统计学的方法，筛选出对违约状态影响最显著的指标。主要有单变量特征选择方法和基于机器学习模型的方法 。 【单变量特征选择 + 基于机器学习】
（5） 模型开发，该步骤主要包括变量分段、变量的WOE（证据权重）变换和逻辑回归估算三部分。【变量离散化(分段) + 变量的woe变换 + 逻辑回归 】
（6） 模型评估，该步骤主要是评估模型的区分能力、预测能力、稳定性，并形成模型评估报告，得出模型是否可以使用的结论。 【K-S指标 + 拟合度曲线】
（7） 信用评分，根据逻辑回归的系数和WOE等确定信用评分的方法。将Logistic模型转换为标准评分的形式。【好坏比 + 拟合度曲线】
（8） 建立评分系统，根据信用评分方法，建立自动信用评分系统。【根据信用评分方法 ，建立评分系统】

1. 数据获取：

数据来自于Kaggle的Give Me Some Credit，有15万条的样本数据，下图可以看到这份数据的大致情况。
数据属于个人消费类贷款，只考虑信用评分最终实施时能够使用到的数据应从如下一些方面获取数据：
– 基本属性：包括了借款人当时的年龄。
– 偿债能力：包括了借款人的月收入、负债比率。
– 信用往来：两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90
天或高于90天逾期的次数。
– 财产状况：包括了开放式信贷和贷款数量、不动产贷款或额度数量。
– 贷款属性：暂无。
– 其他因素：包括了借款人的家属数量（不包括本人在内）。
– 时间窗口：自变量的观察窗口为过去两年，因变量表现窗口为未来两年。

这里的变量有11个，第一个是label，后面10个是自变量，经过后面的IV值筛选后，删除了4，5，6，8，10这5个特征；剩下的有效特征是1，2，3，7，9。

2. 数据预处理：

针对缺失值用RF和直接剔除法进行处理，对于异常值主要根据实际情况和箱型图的数据分布对异常值进行删除。

代码包括缺失值和异常值的处理：

# Missvalue.py
# 数据预处理1：  随机森林处理缺失值。
import pandas as pd
import matplotlib.pyplot as plt #导入图像库
from sklearn.ensemble import RandomForestRegressor

# 用随机森林对缺失值预测填充函数
def set_missing(df):
    # 把已有的数值型特征取出来
    process_df = df.ix[:,[5,0,1,2,3,4,6,7,8,9]]
    # 分成已知该特征和未知该特征两部分
    known = process_df[process_df.MonthlyIncome.notnull()].as_matrix()
    unknown = process_df[process_df.MonthlyIncome.isnull()].as_matrix()
    # X为特征属性值
    X = known[:, 1:]
    # y为结果标签值
    y = known[:, 0]
    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, n_estimators=200,max_depth=3,n_jobs=-1)
    rfr.fit(X, y)
    # 用得到的模型进行未知特征值预测
    predicted = rfr.predict(unknown[:, 1:]).round(0)
    print(predicted)
    # 用得到的预测结果填补原缺失数据
    df.loc[(df.MonthlyIncome.isnull()), 'MonthlyIncome'] = predicted
    return df


if __name__ == '__main__':
    # 载入数据
    data = pd.read_csv('cs-training.csv')
    # 数据集确实和分布情况
    data.describe().to_csv('DataDescribe.csv')  # 了解数据集的分布情况
    data=set_missing(data)  # 用随机森林填补比较多的缺失值
    data=data.dropna()  # 删除比较少的缺失值
    data = data.drop_duplicates()  # 删除重复项
    data.to_csv('MissingData.csv', index=False)
    data.describe().to_csv('MissingDataDescribe.csv')
    """
    #异常值处理
    #年龄等于0的异常值进行剔除
    data=data[data['age']>0]
    # 箱形图
    data379=data[['NumberOfTime30-59DaysPastDueNotWorse','NumberOfTimes90DaysLate','NumberOfTime60-89DaysPastDueNotWorse']]
    data379.boxplot()
    data = data[data['NumberOfTime30-59DaysPastDueNotWorse'] < 90]
    data379 = data[['NumberOfTime30-59DaysPastDueNotWorse', 'NumberOfTimes90DaysLate', 'NumberOfTime60-89DaysPastDueNotWorse']]
    #data379.boxplot()
    plt.show()
    #data.to_csv('PretreatmentData.csv')
    """

# Outlier.py
# 数据预处理2   异常值处理
import pandas as pd
import matplotlib.pyplot as plt #导入图像库
from sklearn.cross_validation import train_test_split

def outlier_processing(df,col):
    s=df[col]
    oneQuoter=s.quantile(0.25)
    threeQuote=s.quantile(0.75)
    irq=threeQuote-oneQuoter
    min=oneQuoter-1.5*irq
    max=threeQuote+1.5*irq
    df=df[df[col]<=max]
    df=df[df[col]>=min]
    return df


if __name__ == '__main__':
    data = pd.read_csv('MissingData.csv')
    # 年龄等于0的异常值进行剔除
    data = data[data['age'] > 0]
    data = data[data['NumberOfTime30-59DaysPastDueNotWorse'] < 90] # 剔除异常值
    data['SeriousDlqin2yrs']=1-data['SeriousDlqin2yrs']
    Y = data['SeriousDlqin2yrs']
    X = data.ix[:, 1:]
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
    # print(Y_train)
    train = pd.concat([Y_train, X_train], axis=1)
    test = pd.concat([Y_test, X_test], axis=1)
    clasTest = test.groupby('SeriousDlqin2yrs')['SeriousDlqin2yrs'].count()
    train.to_csv('TrainData.csv',index=False)
    test.to_csv('TestData.csv',index=False)
    print(train.shape)
    print(test.shape)

3.  探索性分析：

在建立模型之前，我们一般会对现有的数据进行 探索性数据分析（Exploratory Data Analysis） 。 EDA是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索。常用的探索性数据分析方法有：直方图、散点图和箱线图等。
客户年龄分布如图4-1所示，可以看到年龄变量大致呈正态分布，符合统计分析的假设。

客户年收入分布如图4-2所示，月收入也大致呈正态分布，符合统计分析的需要。

4.  变量选择：

特征变量选择(排序)对于数据分析、机器学习从业者来说非常重要。好的特征选择能够提升模型的性能，更能帮助我们理解数据的特点、底层结构，这对进一步改善模型、算法都有着重要作用。至于Python的变量选择代码实现可以参考结合Scikit-learn介绍几种常用的特征选择方法。
在本文中，我们采用信用评分模型的变量选择方法，通过WOE分析方法，即是通过比较指标分箱和对应分箱的违约概率来确定指标是否符合经济意义。首先我们对变量进行离散化（分箱）处理。

  1 分箱处理

变量分箱（binning）是对连续变量离散化（discretization）的一种称呼。信用评分卡开发中一般有常用的等距分段、等深分段、最优分段。其中等距分段（Equval length intervals）是指分段的区间是一致的，比如年龄以十年作为一个分段；等深分段（Equal frequency intervals）是先确定分段数量，然后令每个分段中数据数量大致相等；最优分段（Optimal Binning）又叫监督离散化（supervised discretizaion），使用递归划分（Recursive Partitioning）将连续变量分为分段，背后是一种基于条件推断查找较佳分组的算法。
我们首先选择对连续变量进行最优分段，在连续变量的分布不满足最优分段的要求时，再考虑对连续变量进行等距分段。最优分箱的代码如下：

# part 
# 定义自动分箱函数
def mono_bin(Y, X, n = 20):
    r = 0
    good=Y.sum()
    bad=Y.count()-good
    while np.abs(r) < 1:
        d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
        d2 = d1.groupby('Bucket', as_index = True)
        r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
        n = n - 1
    d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
    d3['min']=d2.min().X
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y
    d3['total'] = d2.count().Y
    d3['rate'] = d2.mean().Y
    d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
    d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
    print("=" * 60)
    print(d4)
    return d4

针对我们将使用最优分段对于数据集中的RevolvingUtilizationOfUnsecuredLines、age、DebtRatio和MonthlyIncome进行分类。

      

 

针对不能最优分箱的变量，分箱如下：

# part  连续变量离散化
    cutx3 = [ninf, 0, 1, 3, 5, pinf]
    cutx6 = [ninf, 1, 2, 3, 5, pinf]
    cutx7 = [ninf, 0, 1, 3, 5, pinf]
    cutx8 = [ninf, 0,1,2, 3, pinf]
    cutx9 = [ninf, 0, 1, 3, pinf]
    cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]

   2 WOE

WoE分析， 是对指标分箱、计算各个档位的WoE值并观察WoE值随指标变化的趋势。其中WoE的数学定义是:
woe=ln(goodattribute/badattribute)
在进行分析时，我们需要对各指标从小到大排列，并计算出相应分档的WoE值。其中正向指标越大，WoE值越小；反向指标越大，WoE值越大。正向指标的WoE值负斜率越大，反响指标的正斜率越大，则说明指标区分能力好。WoE值趋近于直线，则意味指标判断能力较弱。若正向指标和WoE正相关趋势、反向指标同WoE出现负相关趋势，则说明此指标不符合经济意义，则应当予以去除。
woe函数实现在上一节的mono_bin()函数里面已经包含，这里不再重复。

    3 相关性分析和IV筛选

接下来，我们会用经过清洗后的数据看一下变量间的相关性。注意，这里的相关性分析只是初步的检查，进一步检查模型的VI（证据权重）作为变量筛选的依据。
相关性图我们通过Python里面的seaborn包，调用heatmap()绘图函数进行绘制，实现代码如下：

# part
corr = data.corr()#计算各变量的相关性系数
    xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴标签
    yticks = list(corr.index)#y轴标签
    fig = plt.figure()
    ax1 = fig.add_subplot(1, 1, 1)
    sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, annot_kws={'size': 9, 'weight': 'bold', 'color': 'blue'})#绘制相关性系数热力图
    ax1.set_xticklabels(xticks, rotation=0, fontsize=10)
    ax1.set_yticklabels(yticks, rotation=0, fontsize=10)
    plt.show()

生成的图形如图5-5所示：

 

由上图可以看出，各变量之间的相关性是非常小的。NumberOfOpenCreditLinesAndLoans和NumberRealEstateLoansOrLines的相关性系数为0.43。
接下来，我进一步计算每个变量的Infomation Value（IV）。IV指标是一般用来确定自变量的预测能力。 其公式为：
IV=sum((goodattribute-badattribute)*ln(goodattribute/badattribute))
通过IV值判断变量预测能力的标准是：
< 0.02: unpredictive
0.02 to 0.1: weak
0.1 to 0.3: medium
0.3 to 0.5: strong
> 0.5: suspicious
IV的实现放在mono_bin()函数里面，代码实现如下：

# part
# 定义自动分箱函数
def mono_bin(Y, X, n = 20):
    r = 0
    good=Y.sum()
    bad=Y.count()-good
    while np.abs(r) < 1:
        d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
        d2 = d1.groupby('Bucket', as_index = True)
        r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
        n = n - 1
    d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
    d3['min']=d2.min().X
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y
    d3['total'] = d2.count().Y
    d3['rate'] = d2.mean().Y
    d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
    d3['goodattribute']=d3['sum']/good
    d3['badattribute']=(d3['total']-d3['sum'])/bad
    iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
    d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
    print("=" * 60)
    print(d4)
    cut=[]
    cut.append(float('-inf'))
    for i in range(1,n+1):
        qua=X.quantile(i/(n+1))
        cut.append(round(qua,4))
    cut.append(float('inf'))
    woe=list(d4['woe'].round(3))
    return d4,iv,cut,woe

IV代码如下：

# part
ivlist=[ivx1,ivx2,ivx3,ivx4,ivx5,ivx6,ivx7,ivx8,ivx9,ivx10]#各变量IV
    index=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴的标签
    fig1 = plt.figure(1)
    ax1 = fig1.add_subplot(1, 1, 1)
    x = np.arange(len(index))+1
    ax1.bar(x, ivlist, width=0.4)#生成柱状图
    ax1.set_xticks(x)
    ax1.set_xticklabels(index, rotation=0, fontsize=12)
    ax1.set_ylabel('IV(Information Value)', fontsize=14)
    #在柱状图上添加数字标签
    for a, b in zip(x, ivlist):
        plt.text(a, b + 0.01, '%.4f' % b, ha='center', va='bottom', fontsize=10)
    plt.show()

可以看出，DebtRatio、MonthlyIncome、NumberOfOpenCreditLinesAndLoans、NumberRealEstateLoansOrLines和NumberOfDependents变量的IV值明显较低，所以予以删除。

5.  模型分析：

证据权重（Weight of Evidence,WOE）转换可以将Logistic回归模型转变为标准评分卡格式。引入WOE转换的目的并不是为了提高模型质量，只是一些变量不应该被纳入模型，这或者是因为它们不能增加模型值，或者是因为与其模型相关系数有关的误差较大，其实建立标准信用评分卡也可以不采用WOE转换。这种情况下，Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性，但最终得到的评分卡都是一样的。
在建立模型之前，我们需要将筛选后的变量转换为WoE值，便于信用评分。

  1 WOE转换

我们已经能获取了每个变量的分箱数据和woe数据，只需要根据各变量数据进行替换，实现代码如下：

#替换成woe函数
def replace_woe(series,cut,woe):
    list=[]
    i=0
    while i<len(series):
        value=series[i]
        j=len(cut)-2
        m=len(cut)-2
        while j>=0:
            if value>=cut[j]:
                j=-1
            else:
                j -=1
                m -= 1
        list.append(woe[m])
        i += 1
    return list

我们将每个变量都进行替换,并将其保存到WoeData.csv文件中：【训练集和测试集】

# 训练集的替换成woe
    data['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(data['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
    data['age'] = Series(replace_woe(data['age'], cutx2, woex2))
    data['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
    data['DebtRatio'] = Series(replace_woe(data['DebtRatio'], cutx4, woex4))
    data['MonthlyIncome'] = Series(replace_woe(data['MonthlyIncome'], cutx5, woex5))
    data['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(data['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
    data['NumberOfTimes90DaysLate'] = Series(replace_woe(data['NumberOfTimes90DaysLate'], cutx7, woex7))
    data['NumberRealEstateLoansOrLines'] = Series(replace_woe(data['NumberRealEstateLoansOrLines'], cutx8, woex8))
    data['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
    data['NumberOfDependents'] = Series(replace_woe(data['NumberOfDependents'], cutx10, woex10))
    data.to_csv('WoeData.csv', index=False)

    test= pd.read_csv('TestData.csv')
    # 测试集的替换成woe
    test['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(test['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
    test['age'] = Series(replace_woe(test['age'], cutx2, woex2))
    test['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
    test['DebtRatio'] = Series(replace_woe(test['DebtRatio'], cutx4, woex4))
    test['MonthlyIncome'] = Series(replace_woe(test['MonthlyIncome'], cutx5, woex5))
    test['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(test['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
    test['NumberOfTimes90DaysLate'] = Series(replace_woe(test['NumberOfTimes90DaysLate'], cutx7, woex7))
    test['NumberRealEstateLoansOrLines'] = Series(replace_woe(test['NumberRealEstateLoansOrLines'], cutx8, woex8))
    test['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
    test['NumberOfDependents'] = Series(replace_woe(test['NumberOfDependents'], cutx10, woex10))
    test.to_csv('TestWoeData.csv', index=False)

变量选择和模型分析的数据转换的代码整合如下：

# 3  探索分析 + 变量选择 + 模型开发(变量离散化 + 变量的woe变换)
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import scipy.stats.stats as stats
import matplotlib.pyplot as plt
import statsmodels.api as sm
import math

# 变量选择部分的代码
# 定义自动分箱函数
def mono_bin(Y, X, n = 20):
    r = 0
    good=Y.sum()
    bad=Y.count()-good
    while np.abs(r) < 1:
        d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
        d2 = d1.groupby('Bucket', as_index = True)
        r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
        n = n - 1
    d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
    d3['min']=d2.min().X
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y
    d3['total'] = d2.count().Y
    d3['rate'] = d2.mean().Y
    d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
    d3['goodattribute']=d3['sum']/good
    d3['badattribute']=(d3['total']-d3['sum'])/bad
    iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
    d4 = (d3.sort_index(by = 'min'))
    print("=" * 60)
    print(d4)
    cut=[]
    cut.append(float('-inf'))
    for i in range(1,n+1):
        qua=X.quantile(i/(n+1))
        cut.append(round(qua,4))
    cut.append(float('inf'))
    woe=list(d4['woe'].round(3))
    return d4,iv,cut,woe


# 自定义分箱函数
def self_bin(Y,X,cat):
    good=Y.sum()
    bad=Y.count()-good
    d1=pd.DataFrame({'X':X,'Y':Y,'Bucket':pd.cut(X,cat)})
    d2=d1.groupby('Bucket', as_index = True)
    d3 = pd.DataFrame(d2.X.min(), columns=['min'])
    d3['min'] = d2.min().X
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y
    d3['total'] = d2.count().Y
    d3['rate'] = d2.mean().Y
    d3['woe'] = np.log((d3['rate'] / (1 - d3['rate'])) / (good / bad))
    d3['goodattribute'] = d3['sum'] / good
    d3['badattribute'] = (d3['total'] - d3['sum']) / bad
    iv = ((d3['goodattribute'] - d3['badattribute']) * d3['woe']).sum()
    d4 = (d3.sort_index(by='min'))
    print("=" * 60)
    print(d4)
    woe = list(d4['woe'].round(3))
    return d4, iv,woe

# 模型分析开始的代码
# 用woe代替
def replace_woe(series,cut,woe):
    list=[]
    i=0
    while i<len(series):
        value=series[i]
        j=len(cut)-2
        m=len(cut)-2
        while j>=0:
            if value>=cut[j]:
                j=-1
            else:
                j -=1
                m -= 1
        list.append(woe[m])
        i += 1
    return list


# 计算分数函数
def get_score(coe,woe,factor):
    scores=[]
    for w in woe:
        score=round(coe*w*factor,0)
        scores.append(score)
    return scores

# 根据变量计算分数
def compute_score(series,cut,score):
    list = []
    i = 0
    while i < len(series):
        value = series[i]
        j = len(cut) - 2
        m = len(cut) - 2
        while j >= 0:
            if value >= cut[j]:
                j = -1
            else:
                j -= 1
                m -= 1
        list.append(score[m])
        i += 1
    return list

if __name__ == '__main__':
    data = pd.read_csv('TrainData.csv')
    pinf = float('inf')  # 正无穷大
    ninf = float('-inf')  # 负无穷大
    dfx1, ivx1,cutx1,woex1=mono_bin(data.SeriousDlqin2yrs,data.RevolvingUtilizationOfUnsecuredLines,n=10)
    dfx2, ivx2,cutx2,woex2=mono_bin(data.SeriousDlqin2yrs, data.age, n=10)
    dfx4, ivx4,cutx4,woex4 =mono_bin(data.SeriousDlqin2yrs, data.DebtRatio, n=20)
    dfx5, ivx5,cutx5,woex5 =mono_bin(data.SeriousDlqin2yrs, data.MonthlyIncome, n=10)
    # 连续变量离散化
    cutx3 = [ninf, 0, 1, 3, 5, pinf]
    cutx6 = [ninf, 1, 2, 3, 5, pinf]
    cutx7 = [ninf, 0, 1, 3, 5, pinf]
    cutx8 = [ninf, 0,1,2, 3, pinf]
    cutx9 = [ninf, 0, 1, 3, pinf]
    cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]
    dfx3, ivx3,woex3 = self_bin(data.SeriousDlqin2yrs, data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3)
    dfx6, ivx6 ,woex6= self_bin(data.SeriousDlqin2yrs, data['NumberOfOpenCreditLinesAndLoans'], cutx6)
    dfx7, ivx7,woex7 = self_bin(data.SeriousDlqin2yrs, data['NumberOfTimes90DaysLate'], cutx7)
    dfx8, ivx8,woex8 = self_bin(data.SeriousDlqin2yrs, data['NumberRealEstateLoansOrLines'], cutx8)
    dfx9, ivx9,woex9 = self_bin(data.SeriousDlqin2yrs, data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9)
    dfx10, ivx10,woex10 = self_bin(data.SeriousDlqin2yrs, data['NumberOfDependents'], cutx10)
    ivlist=[ivx1,ivx2,ivx3,ivx4,ivx5,ivx6,ivx7,ivx8,ivx9,ivx10]
    index=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
    fig1 = plt.figure(1)
    ax1 = fig1.add_subplot(1, 1, 1)
    x = np.arange(len(index))+1
    ax1.bar(x, ivlist, width=0.4)
    ax1.set_xticks(x)
    ax1.set_xticklabels(index, rotation=0, fontsize=12)
    ax1.set_ylabel('IV(Information Value)', fontsize=14)
    for a, b in zip(x, ivlist):
        plt.text(a, b + 0.01, '%.4f' % b, ha='center', va='bottom', fontsize=10)
    # 训练集的替换成woe
    data['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(data['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
    data['age'] = Series(replace_woe(data['age'], cutx2, woex2))
    data['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
    data['DebtRatio'] = Series(replace_woe(data['DebtRatio'], cutx4, woex4))
    data['MonthlyIncome'] = Series(replace_woe(data['MonthlyIncome'], cutx5, woex5))
    data['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(data['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
    data['NumberOfTimes90DaysLate'] = Series(replace_woe(data['NumberOfTimes90DaysLate'], cutx7, woex7))
    data['NumberRealEstateLoansOrLines'] = Series(replace_woe(data['NumberRealEstateLoansOrLines'], cutx8, woex8))
    data['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
    data['NumberOfDependents'] = Series(replace_woe(data['NumberOfDependents'], cutx10, woex10))
    data.to_csv('WoeData.csv', index=False)

    test= pd.read_csv('TestData.csv')
    # 测试集的替换成woe
    test['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(test['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
    test['age'] = Series(replace_woe(test['age'], cutx2, woex2))
    test['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
    test['DebtRatio'] = Series(replace_woe(test['DebtRatio'], cutx4, woex4))
    test['MonthlyIncome'] = Series(replace_woe(test['MonthlyIncome'], cutx5, woex5))
    test['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(test['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
    test['NumberOfTimes90DaysLate'] = Series(replace_woe(test['NumberOfTimes90DaysLate'], cutx7, woex7))
    test['NumberRealEstateLoansOrLines'] = Series(replace_woe(test['NumberRealEstateLoansOrLines'], cutx8, woex8))
    test['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
    test['NumberOfDependents'] = Series(replace_woe(test['NumberOfDependents'], cutx10, woex10))
    test.to_csv('TestWoeData.csv', index=False)

    # 计算分数
    # coe为逻辑回归模型的系数
    coe=[9.738849,0.638002,0.505995,1.032246,1.790041,1.131956]
    # 我们取600分为基础分值，PDO为20（每高20分好坏比翻一倍），好坏比取20。
    p = 20 / math.log(2)
    q = 600 - 20 * math.log(20) / math.log(2)
    baseScore = round(q + p * coe[0], 0)
    # 各项部分分数
    x1 = get_score(coe[1], woex1, p)
    x2 = get_score(coe[2], woex2, p)
    x3 = get_score(coe[3], woex3, p)
    x7 = get_score(coe[4], woex7, p)
    x9 = get_score(coe[5], woex9, p)
    print(x1,x2, x3, x7, x9)
    test1 = pd.read_csv('TestData.csv')
    test1['BaseScore']=Series(np.zeros(len(test1)))+baseScore
    test1['x1'] = Series(compute_score(test1['RevolvingUtilizationOfUnsecuredLines'], cutx1, x1))
    test1['x2'] = Series(compute_score(test1['age'], cutx2, x2))
    test1['x3'] = Series(compute_score(test1['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3))
    test1['x7'] = Series(compute_score(test1['NumberOfTimes90DaysLate'], cutx7, x7))
    test1['x9'] = Series(compute_score(test1['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, x9))
    test1['Score'] = test1['x1'] + test1['x2'] + test1['x3'] + test1['x7'] +test1['x9']  + baseScore
    test1.to_csv('ScoreData.csv', index=False)
    plt.show()

   2 Logisic模型建立

我们直接调用statsmodels包来实现逻辑回归：

    导入数据
    data = pd.read_csv('WoeData.csv')
    #应变量
    Y=data['SeriousDlqin2yrs']
    #自变量，剔除对因变量影响不明显的变量
    X=data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
    X1=sm.add_constant(X)
    logit=sm.Logit(Y,X1)
    result=logit.fit()
    print(result.summary())

 

通过图6-1可知，逻辑回归各变量都已通过显著性检验，满足要求。

   3 模型检验

到这里，我们的建模部分基本结束了。我们需要验证一下模型的预测能力如何。我们使用在建模开始阶段预留的test数据进行检验。通过ROC曲线和AUC来评估模型的拟合能力。
在Python中，可以利用sklearn.metrics，它能方便比较两个分类器，自动计算ROC和AUC。
实现代码：

    #因变量
    Y_test = test['SeriousDlqin2yrs']
    #自变量，剔除对因变量影响不明显的变量，与模型变量对应
    X_test = test.drop(['SeriousDlqin2yrs', 'DebtRatio', 'MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines', 'NumberOfDependents'], axis=1)
    X3 = sm.add_constant(X_test)
    resu = result.predict(X3)#进行预测
    fpr, tpr, threshold = roc_curve(Y_test, resu)
    rocauc = auc(fpr, tpr)#计算AUC
    plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)#生成ROC曲线
    plt.legend(loc='lower right')
    plt.plot([0, 1], [0, 1], 'r--')
    plt.xlim([0, 1])
    plt.ylim([0, 1])
    plt.ylabel('真正率')
    plt.xlabel('假正率')
    plt.show()

结果图，AUC值为0.85，说明该模型的预测效果还是不错的，正确率较高。

训练逻辑回归模型和在测试集上进行验证的代码：

# 4 根据处理后的数据集进行逻辑回归模型的训练，然后基于训练好的模型进行测试效果。
import pandas as pd
import matplotlib.pyplot as plt  # 导入图像库
import matplotlib
import seaborn as sns
import statsmodels.api as sm
from sklearn.metrics import roc_curve, auc

if __name__ == '__main__':
    # 先根据替换成woe后的数据集WoeData.csv进行逻辑回归的训练
    matplotlib.rcParams['axes.unicode_minus'] = False
    data = pd.read_csv('WoeData.csv')
    Y=data['SeriousDlqin2yrs']
    X=data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
    X1=sm.add_constant(X)
    logit=sm.Logit(Y,X1)
    result=logit.fit()
    print(result.params)

    # 然后测试集TestWoeData.csv上进行上述训练好的逻辑回归模型的测试效果
    test = pd.read_csv('TestWoeData.csv')
    Y_test = test['SeriousDlqin2yrs']
    X_test = test.drop(['SeriousDlqin2yrs', 'DebtRatio', 'MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines', 'NumberOfDependents'], axis=1)
    X3 = sm.add_constant(X_test)
    resu = result.predict(X3)
    fpr, tpr, threshold = roc_curve(Y_test, resu)
    rocauc = auc(fpr, tpr)
    plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
    plt.legend(loc='lower right')
    plt.plot([0, 1], [0, 1], 'r--')
    plt.xlim([0, 1])
    plt.ylim([0, 1])
    plt.ylabel('真正率')
    plt.xlabel('假正率')
    plt.show()

6.建立统一的信用卡评分系统：

将逻辑回归模型转换成标准评分卡的形式。